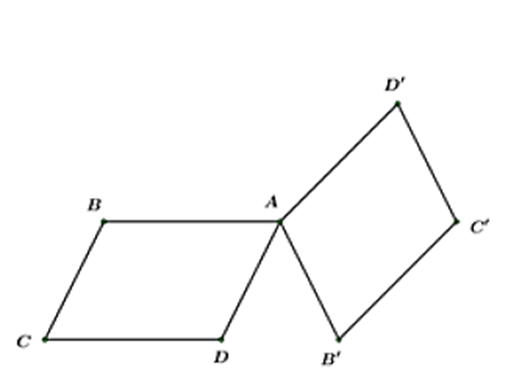
Cho hai hình bình hành ABCD và AB′C′D′ có chung đỉnh A. Khẳng định nào đúng
Cho hai hình bình hành ABCD và AB′C′D′ có chung đỉnh A. Khẳng định nào đúng?
A. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {AC} \].
B. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow 0 \].
C. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {BC} \].
D. \[\overrightarrow {B'B} + \overrightarrow {CC'} + \overrightarrow {D'D} = \overrightarrow {BD} \].