Cho hai hàm số y = −x + 3 và y = 3x − 1 có đồ thị lần lượt là hai đường thẳng d1 và d2.
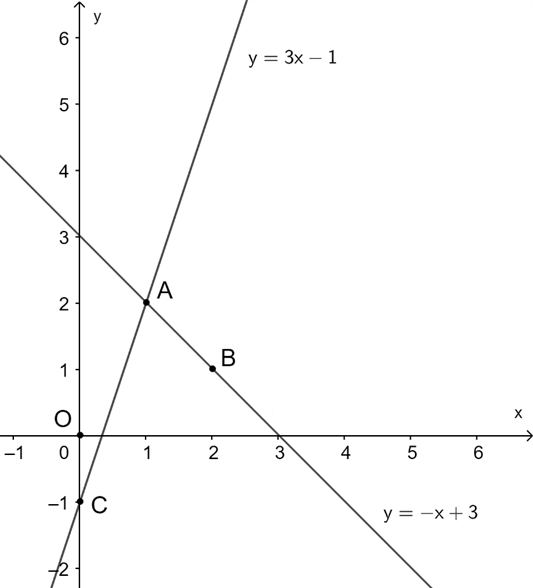
a) Vẽ d1 và d2 trên cùng một hệ trục tọa độ.
b) Tính góc tạo bởi d1, d2 và trục Ox (làm tròn đến độ).
d) Tính khoảng cách từ O đến d1, d2.
a) +) Lấy hai điểm thuộc d1.
• x = 1 Þ y = 2 nên ta có điểm A(1; 2).
• x = 2 Þ y = 1 nên ta có điểm B(2; 1).
+) Lấy hai điểm thuộc d2.
• x = 1 Þ y = 2 nên ta có điểm A(1; 2).
• x = 0 Þ y = −1 nên ta có điểm C(0; −1).
b) Tọa độ giao điểm là nghiệm của hệ phương trình
\[\left\{ \begin{array}{l}y = - x + 3\\y = 3x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\\3x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right. \Rightarrow A\left( {1;\;2} \right)\]
c) Ta có: \[\tan {\alpha _1} = {a_1} = - 1 \Rightarrow - {\alpha _1} = 45^\circ \].
Và \(\tan {\alpha _2} = {a_2} = 3 \Rightarrow {\alpha _2} \approx 71,565^\circ \).
Vậy \[\alpha = 180^\circ - 45^\circ - 71,565^\circ \approx 63^\circ \].
d) Khoảng cách từ O đến d1 là:
\({d_{O/{d_1}}} = \frac{{\left| 3 \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{1}{{\sqrt 2 }}\).
Khoảng cách từ O đến d2 là:
\({d_{O/{d_2}}} = \frac{{\left| { - 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = \frac{1}{{\sqrt {10} }}\).