Cho hai hàm số $\text{f}\left(\text{x}\right)={\text{ax}}^3+{\text{bx}}^2+\text{cx}+\text{d},(\text{a}\ne 0)$ và $\text{g}\left(\text{x}\right)={\text{mxx}}^2+\text{nx}+\text{p},(\text{m}\ne 0)$ có đồ thị cắt nhau tại 3 điểm có hoành độ $x_1,x_2,x_3$ (như hình vẽ).

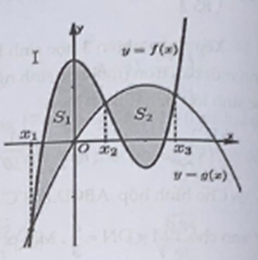
Ký hiệu ${\text{S}}_1, {\text{S}}_2$lần lượt là diện tích các hình phẳng giới hạn bới đồ thị hàm số y = f(x) và y = g(x)(phần tô đậm). Biết $S_1=10,S_2=7$. Tính ${\int }_{x1}^{x3}\left[f\left(x\right)-g\left(x\right)\right]\text{dx}$ 

Ta có: $S_1=\underset{x1}{\overset{x2}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx;S_2=\underset{x2}{\overset{x3}{\int }}\left[g\left(x\right)-f\left(x\right)\right]dx$

Ta có $\underset{x1}{\overset{x3}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx=\underset{x1}{\overset{x2}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx+\underset{x2}{\overset{x3}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx$