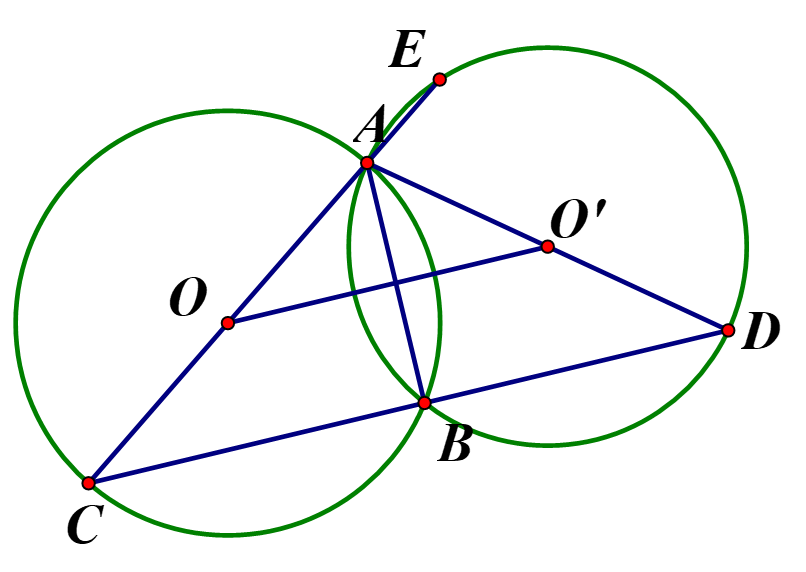
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A, và B. Kẻ các
Cho hai đường tròn bằng nhau \(\left( O \right)\)và \(\left( {O'} \right)\)cắt nhau tại hai điểm \(A\)và B. Kẻ các đường kính \(AOC,AO'D.\)Gọi E là giao điểm thứ hai của \(AC\)với đường tròn \(\left( {O'} \right)\)
a) So sánh các cung nhỏ \(BC,BD\)
b) Chứng minh rằng B là điểm chính giữa của cung \(EBD\)(tức là điểm B chia cung thành hai cung bằng nhau