cho hai đường thẳng: y = x + 3 (d1), y = 3x + 7 (d2). a) Vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ Oxy. b) Gọi giao điểm của đường thẳng (d1) và (d2) với trục Oy lần lượt l
cho hai đường thẳng: y = x + 3 (d1), y = 3x + 7 (d2).
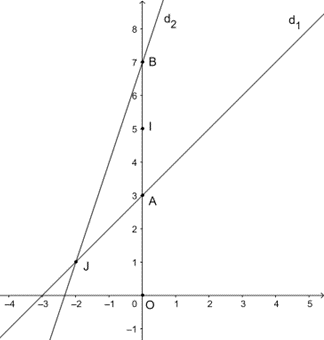
a) Vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ Oxy.
b) Gọi giao điểm của đường thẳng (d1) và (d2) với trục Oy lần lượt là A và B. Tìm tọa độ trung điểm I của đoạn AB.
c) Gọi J là giao điểm của hai đường thẳng (d1) và (d2). Chứng minh tam giác OIJ là tam giác vuông. Tính diện tích của tam giác đó.
a) Vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ Oxy.
b) Gọi giao điểm của đường thẳng (d1) và (d2) với trục Oy lần lượt là A và B. Tìm tọa độ trung điểm I của đoạn AB.
c) Gọi J là giao điểm của hai đường thẳng (d1) và (d2). Chứng minh tam giác OIJ là tam giác vuông. Tính diện tích của tam giác đó.