Cho hai đường thẳng \(\left( {{D_1}} \right):y = \frac{1}{2}x + 2\) và \(\left( {{D_2}} \right):y = - x + 2\)

Gọi A và B theo thứ tự giao điểm của (D₁) và (D₂) với các trục hoành, C là giao điểm của hai đường thẳng đó (đơn vị trên các trục tọa độ là centimet).

Khẳng định nào sau đây sai?

Lời giải

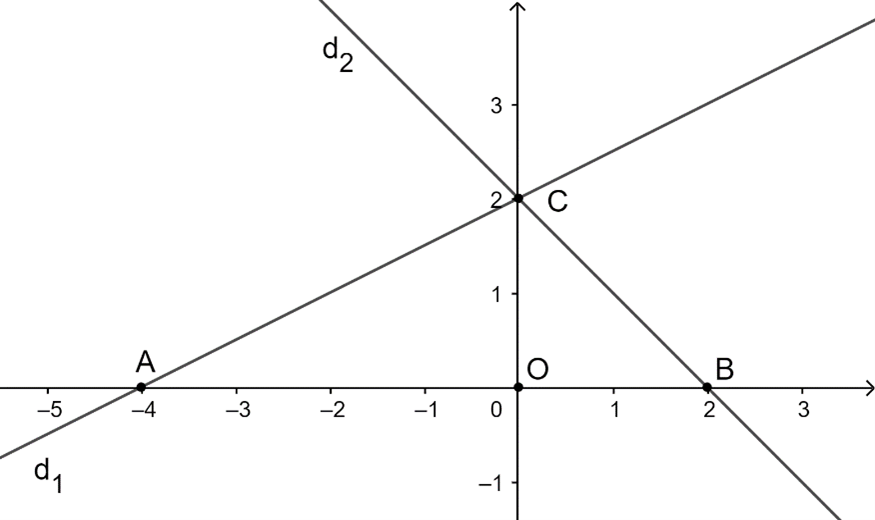
• Vì A là giao điểm của (D₁) với trục hoành nên hoành độ giao điểm của A là nghiệm của phương trình:

\(\frac{1}{2}x + 2 = 0 \Leftrightarrow x = - 4\)

Khi đó, tọa độ của điểm A là A(– 4, 0).

Þ OA = 8 (cm)

• Vì B là giao điểm của (D₂) với trục hoành nên hoành độ giao điểm của A là nghiệm của phương trình:

– x + 2 = 0 Û x = 2

Khi đó, tọa độ của điểm B là B(2, 0).

Þ OB = 2 (cm)

• Vì C là giao điểm của hai đường thẳng (D₁) và (D₂) nên hoành độ giao điểm của C là nghiệm của phương trình:

\(\frac{1}{2}x + 2 = - x + 2 \Leftrightarrow x = 0\)

Khi đó, tọa độ của điểm C là C(0; 2).

Þ OC = 2 (cm)

Xét khẳng định A.

\(\tan A = \frac{{OC}}{{OA}} = \frac{2}{4} = \frac{1}{2} \Rightarrow \widehat A = 26^\circ 33'.\)

\(\tan B = \frac{{OC}}{{OB}} = \frac{2}{2} = 1 \Rightarrow \widehat B = 45^\circ .\)

Do đó \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {26^\circ 33' + 45^\circ } \right) = 108^\circ 27'.\)

Vậy khẳng định A đúng.

Xét khẳng định B.

Ta có AB = 6 (cm).

Theo định lí Py-ta-go, ta có:

AC² = OA² + OC² = 4² + 2² = 20

\( \Rightarrow AC = \sqrt {20} = 4,47\;\left( {cm} \right).\)

Theo định lí Py-ta-go, ta có:

BC² = OB² + OC² = 2² + 2² = 8

\( \Rightarrow BC = \sqrt 8 = 2,83\;\left( {cm} \right).\)

Chu vi tam giác ABC là:

P_∆ABC = AB + AC + BC

= 6 + 4,47 + 2,83 = 13,3 (cm).

Vậy khẳng định B sai.

Xét khẳng định C.

Diện tích tam giác ABC là:

\({S_{ABC}} = \frac{1}{2}AB.OC = \frac{1}{2}.6.2 = 6\;\left( {c{m^2}} \right)\)

Vậy khẳng định C đúng.

Vậy ta chọn đáp án B.