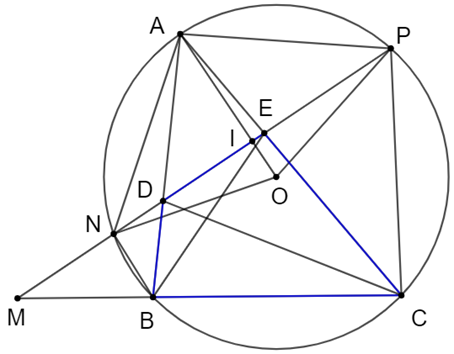
Cho đường tròn tâm O và BC là dây cung không đi qua tâm. Trên tia đối của tia BC lấy điểm M sao cho M không trùng với B. Đường thẳng đi qua M cắt đường tròn (O) đã cho tại N và P

Trả lời

a) Gọi I là giao điểm của OA và NP

Ta có độ dài cung AN bằng độ dài cung AP nên suy ra AN = AP

Và ON = OP = R.

=> OA là đường trung trực của đoạn thẳng NP

=> OA $\perp$ NP tại I

=> $\widehat{AID}=90°\Rightarrow \widehat{ADI}=90°-\widehat{IAD}$

Hay $\widehat{ADP}=90°-\widehat{OAB}$

Lại có: OA = OB => ∆OAB cân tại O.

$\Rightarrow \widehat{OAB}=\frac{180°-\widehat{AOB}}{2}=90°-\frac{\widehat{AOB}}{2}$

Suy ra $\widehat{ADP}=90°-\left(90°-\frac{\widehat{AOB}}{2}\right)=\frac{\widehat{AOB}}{2}$

Mà $\widehat{MDB}=\widehat{ADP}$ (Hai góc đối đỉnh) $\Rightarrow \widehat{MDB}=\frac{\widehat{AOB}}{2}$

Đường tròn (O) có:  là góc nội tiếp chắn cung AB và  là góc ở tâm chắn cung AB nên suy ra: $\widehat{ACB}=\frac{\widehat{AOB}}{2}\Rightarrow \widehat{ACB}=\widehat{MDB}$

Hay $\widehat{ECB}=\widehat{MDB}$

Tứ giác BNDC có $\widehat{ECB}+\widehat{EDB}=\widehat{MDB}+\widehat{EDB}=\widehat{MDE}=180°$

Suy ra BNDC là tứ giác nội tiếp.