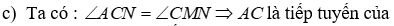Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại K (K nằm giữa A và O)
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại K (K nằm giữa A và O). Lấy điểm M trên cung nhỏ BC (M khác B và C). AM cắt CD tại N. Chứng minh:
a) BMNK là tứ giác nội tiếp đường tròn.
b) KA.KB = KC.KD và AMAN = AC2
c) Khi M chạy trên cun nhỏ BC thì tâm đường tròn ngoại tiếp tam giác CMN luôn thuộc một đường thẳng cố định.
