Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC (E khác B và C), AE cắt CD tại F. Chứng minh:

a) BEFI là tứ giác nội tiếp đường tròn.

b) AE . AF = AC².

c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.

Lời giải

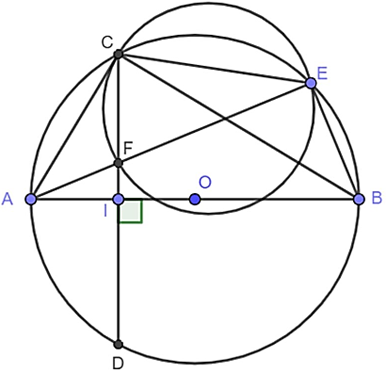
a) Tứ giác BEFI có: $\widehat {BIF} = 90^\circ$ (giả thiết)

Suy ra I thuộc đường tròn đường kính BF.

$\widehat {BEF} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Nên E thuộc đường tròn đường kính BF

Þ BEFI nội tiếp đường tròn đường kính BF.

b) AB ^ CD

• Xét ∆OCD cân có OI là đường cao nên cũng là đường trung tuyến, nên I là trung điểm của CD.

• Xét ∆ACD có AI vừa là đường cao vừa là đường trung tuyến nên ∆ACD cân tại đỉnh A nên AC = AD

Þ $\widehat {ACF} = \widehat {AEC}$ (hai góc nội tiếp chắn hai cung bằng nhau)

Xét ∆ACF và ∆AEC có:

$\widehat A$ chung

$\widehat {ACF} = \widehat {AEC}$ (cmt)

Þ ∆ACF ᔕ ∆AEC (g.g)

$\Rightarrow \frac{{AC}}{{AE}} = \frac{{AF}}{{AC}}$ (hai cạnh tương ứng tỉ lệ)

Þ AE . AF = AC²

c) $\widehat {ACF} = \widehat {AEC}$ Þ AC là tiếp tuyến đường tròn ngoại tiếp ∆CEF (1)

Mặt khác $\widehat {ACB} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)

Þ AC ^ CB (2)

Từ (1) và (2) suy ra CB chứa đường kính đường tròn ngoại tiếp ∆CEF

Mà CB cố định nên tâm đường tròn ngoại tiếp ∆CEF thuộc CB cố định khi E thay đổi trên cung nhỏ BC.