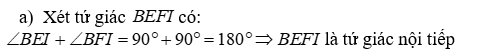Cho đường tròn tâm \(O\)đường kính \(AB\). Vẽ dây cung \(CD\) vuông góc với \(\)\(AB\) tại \(I(I\)nằm giữa \(A\)và \(O)\).Lấy điểm \(E\)tren cung nhỏ khác \(B\)và \(C),AE\)cắt \(CD\)tại \(F.\)Chứng minh :\(BC(E\)

a.        là tứ giác nội tiếp đường tròn.

b.     \(IA.IB = IC.ID\) và \(AE.AF = A{C^2}\)

c.      Khi \(E\) chạy trên cun nhỏ \(BC\)thì tâm đường tròn ngoại tiếp \(\Delta CEF\) luôn thuộc một đường thẳng cố định.