Cho đường tròn tâm O, đường kính AB và điểm C thuộc đường tròn sao cho AC > BC. Qua O vẽ đường thẳng vuông góc với dây AC ở H. Kẻ tiếp tuyến tại A của đường tròn cắt tia OH ở D. BD cắt đường
33
12/05/2024
Cho đường tròn tâm O, đường kính AB và điểm C thuộc đường tròn sao cho AC > BC. Qua O vẽ đường thẳng vuông góc với dây AC ở H. Kẻ tiếp tuyến tại A của đường tròn cắt tia OH ở D. BD cắt đường tròn tâm O ở E.
a) Chứng minh HA = HC.
b) Biết \[\widehat {DCO} = 90^\circ \]. Chứng minh OH . DO = DE . DB.
c) Trên tia đối của EA lấy F sao cho E là trung điểm AF. Từ F vẽ đường thẳng AD vuông góc ở K; KF cắt BC ở M. Chứng minh MK = MF.
Trả lời
Lời giải
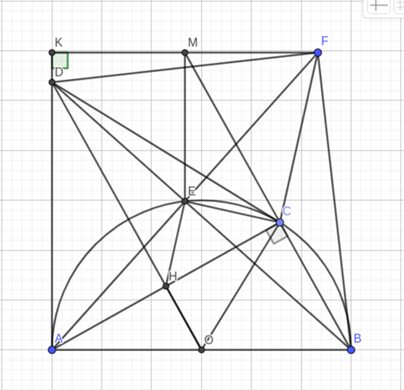
a) Vì A, C ∈ (O); OH ⊥ AC ⇒ H là trung điểm của AC ⇒ HA = HC
Do AH = HC, DO ⊥ AC ⇒ DO là đường trung trực của AC
b) Vì \[\widehat {DCO}\] = 90°, CH ⊥ DO ⇒ DC2 = DH . DO
Mà ∆DCE ᔕ ∆DBC (g.g).
Suy ra DE . DB = DC2
Do đó DH . DO = DE . DB.
c) Ta có E là trung điểm AF, H là trung điểm AC là đường trung bình.
Mà tứ giác ADEH nội tiếp do \[\widehat {DEA} = \widehat {DHA} = 90^\circ \].
Lại có \[\widehat {FED} = \widehat {CBA} = \widehat {DOA}\] ⇒ \[\widehat {DAO} = \widehat {FCE}\] = 90°
Mặt khác: FK // AB ⇒ \[\widehat {FMC} = \widehat {MBA} = \widehat {FEC}\]
\[\widehat {EMF} + \widehat {EFC}\] = 90° ⇒ \[\widehat {EFM}\] = 90° ⇒ EM // AK.
Do đó M là trung điểm của KF (E là trung điểm của AC).

