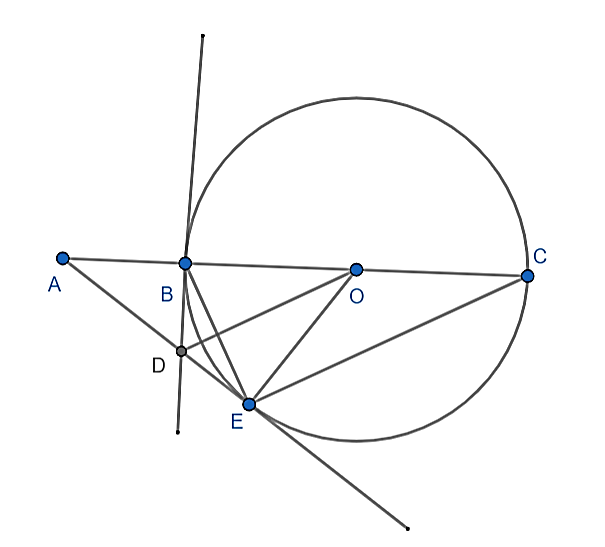
Cho đường tròn tâm (O) có đường kính BC. Kẻ tiếp tuyến Bx với nửa đường tròn (O). Trên tia đối của CB lấy điểm A. Kẻ tiếp tuyến AE với nửa đường tròn, tia AE cắt Bx tại D (Bx nằm trên nửa mặt phẳng bờ BC chứa nửa đường tròn (O)).

a) Chứng minh: DO // EC.

b) Chứng minh: AO.AB = AE.AD.

a) Ta có: BD, DE là hai tiếp tuyến của đường tròn (O)

$\widehat{BOD}=\widehat{DBE}=\frac{1}{2}\stackrel{⏜}{BE}$

Ta có: $\widehat{BDO}+\widehat{BOD}=90°$

Suy ra: $\widehat{BDO}+\widehat{DBE}=90°$

Hay: BE ⊥ DO (1)

Ta có: $\widehat{BDO}=\widehat{EDO}$

$\widehat{BEC}$= 90° vì ∆BEC là tam giác nội tiếp nửa đường tròn.

Suy ra: BE ⊥ EC (2)

Từ (1) và (2) suy ra: DO // EC

b) Xét ∆AEO và ∆ABD có:

Chung $\widehat{A}$

$\widehat{ABD}=\widehat{AEO}$

⇒∆AEO ~ ∆ABD (g.g)

⇒ $\frac{AO}{AD}=\frac{AE}{AB}$

⇒ AO.AB = AE.AD