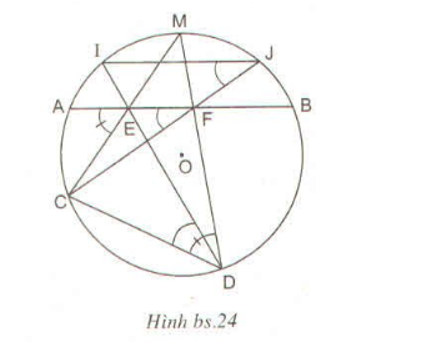
Cho đường tròn tâm O bán kỉnh và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB ?

Xem hình vẽ (h.bs.24)

Ta có cung AM và MB bằng nhau nên $\widehat{AEC}=\widehat{CDM}$ (cùng bằng nửa số đo của cung nhỏ CM)

Suy ra CDFE là tứ giác nội tiếp

Từ đó $\widehat{CDE}=\widehat{CFE}$ (cùng chắn cung CE)

Lại có $\widehat{IJC}=\widehat{IDC}$ (cùng chắn cung CI)

Vậy _{$\widehat{IJC}=\widehat{AFC}$}, suy ra JI song song với AB