Cho đường tròn tâm O, bán kính R = 8 cm và một điểm A có khoảng cách OA = 16 cm. Một đường kính BC quay xung quanh tâm O (đường thẳng BC không đi qua A). Đường tròn ngoại tiếp tam giác ABC cắ
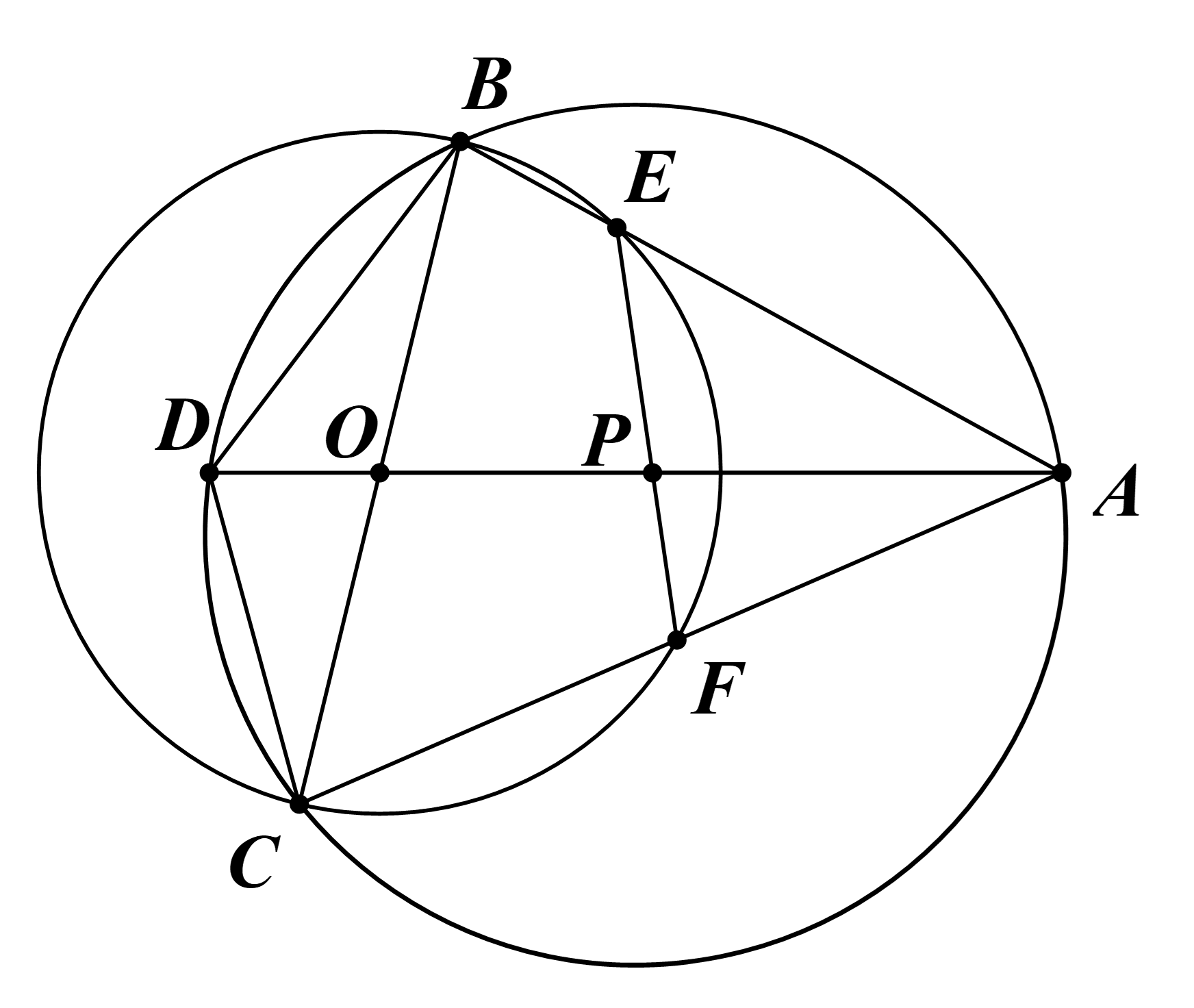
Cho đường tròn tâm O, bán kính R = 8 cm và một điểm A có khoảng cách OA = 16 cm. Một đường kính BC quay xung quanh tâm O (đường thẳng BC không đi qua A). Đường tròn ngoại tiếp tam giác ABC cắt đường thẳng OA tại điểm thứ hai là D.
a) Chứng minh ∆OAB và ∆OCD đồng dạng.
b) Tính OD, suy ra D là điểm cố định khi đường kính BC quay xung quanh điểm O.
c) Giả sử AB cắt đường tròn (O) tại điểm thứ hai E và AC cắt đường tròn (O) tại điểm thứ hai F và gọi P là giao điểm của EF với OA. Chứng minh bốn điểm C, F, D, P cùng nằm trên một đường tròn. Có nhận xét gì về bốn điểm B, E, D, P?