Cho đường tròn (O) và điểm I không nằm trên đường tròn. Qua điểm I kẻ 2 dây
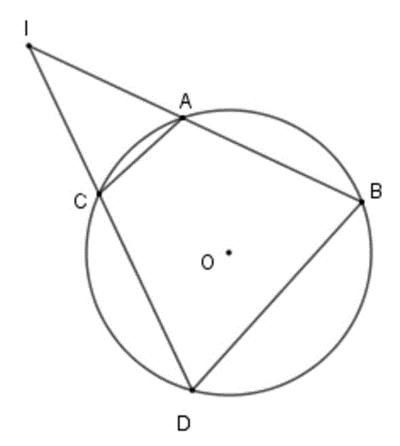
Cho đường tròn (O) và điểm I không nằm trên đường tròn. Qua điểm I kẻ 2 dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D.
a) So sánh các cặp góc ^ACI và ^ABD, ^CAI và ^CDB.
b) Chứng minh các tam giác IAC và IDB đồng dạng.
c) Chứng minh IA.IB = IC. ID.