Cho đường tròn (O; R). Vẽ 2 dây AB và CD vuông góc với nhau. Chứng minh SACBD ≤ 2R^2.

Trả lời

Lời giải

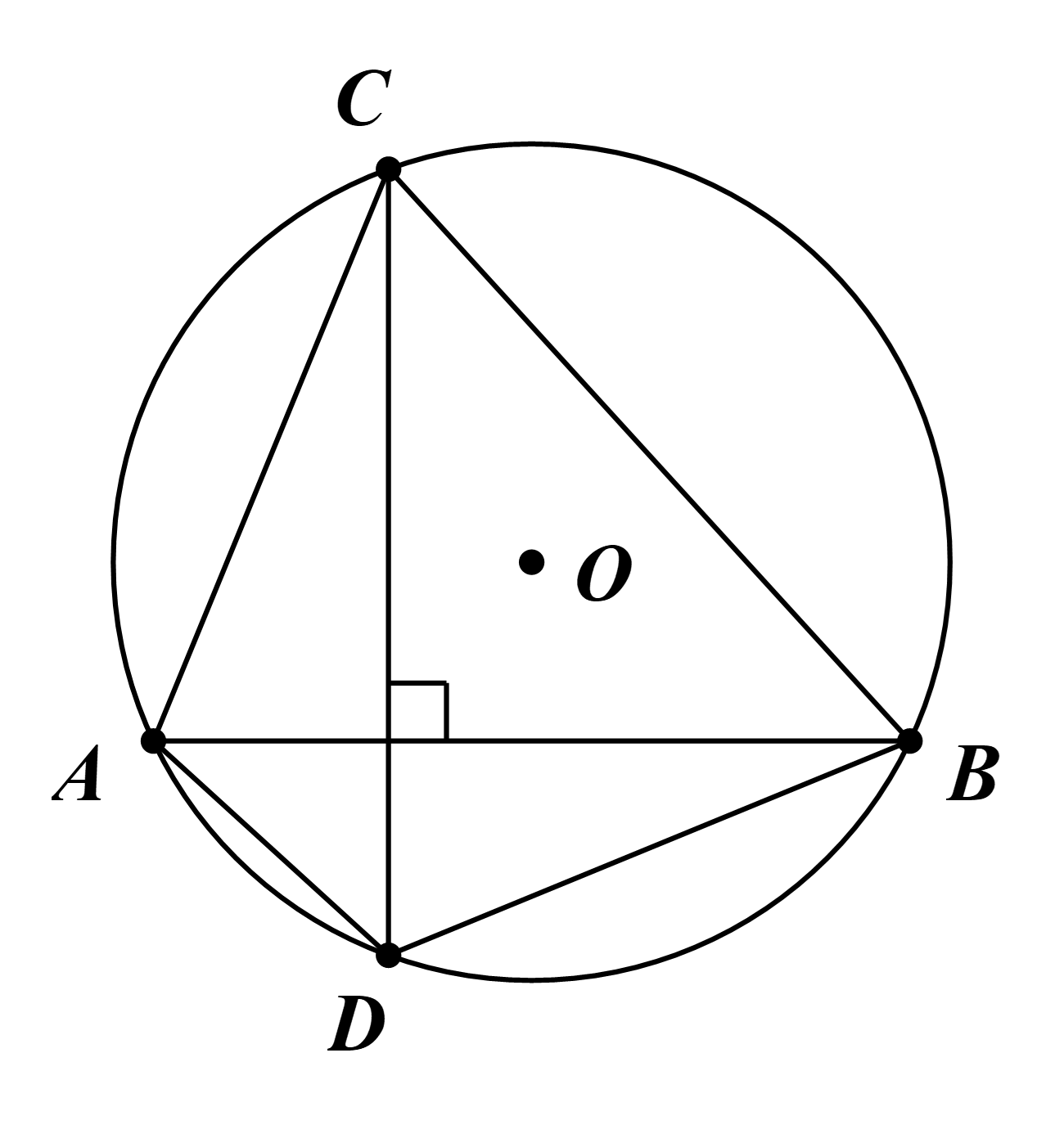
Vì AB, CD là các dây của đường tròn (O; R) nên AB ≤ 2R và CD ≤ 2R.

Vì AB ⊥ CD nên ${S_{ABCD}} = \frac{1}{2}AB.CD \le \frac{1}{2}.2R.2R = 2{R^2}$.

Vậy ta có điều phải chứng minh.