Cho đường tròn (O ; R) và một điểm A sao cho OA = 2R vẽ các tiếp tuyến AB, AC với (O;R) , B và C là các tiếp điểm. Vẽ đường kính BOD.

a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.

b) Chứng minh DC // OA.

c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh OCEA là hình thang cân.

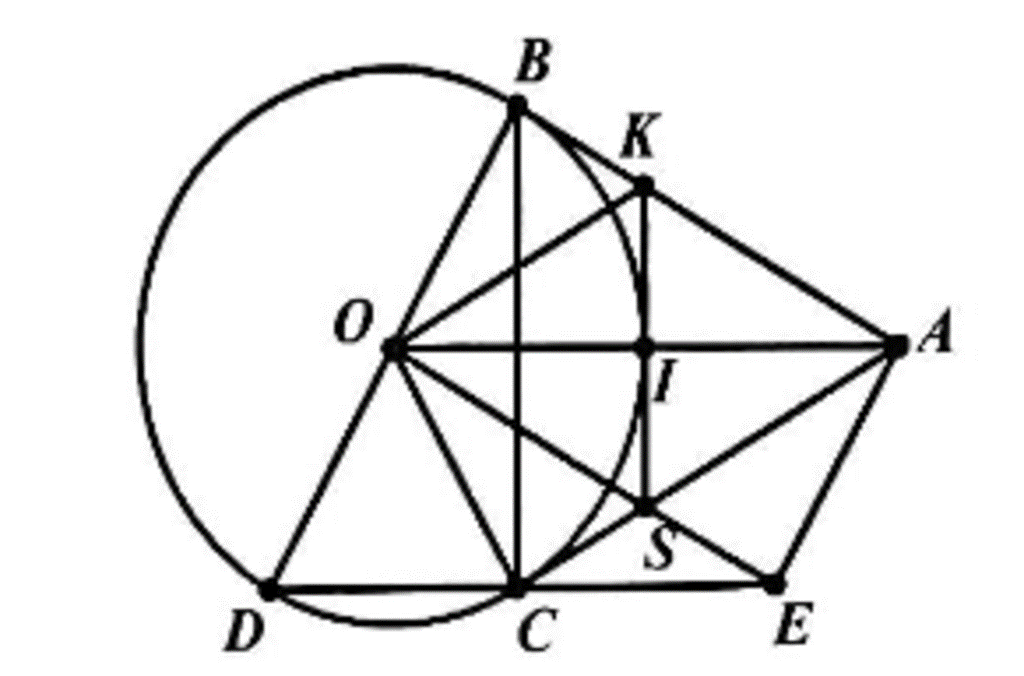
a) AB, AC là tiếp tuyến của (O) nên $\widehat{OBA}=\widehat{OCA}$  = 90°

⇒ B, C cùng thuộc đường tròn đường kính OA 

⇒ A, B, C, O cùng thuộc đường tròn đường kính OA

b) AB, AC là tiếp tuyến của (O) ⇒ AB = AC mà OB = OC = R  

⇒ OA là trung trực BC ⇒ OA⊥ BC 

ΔBCD nội tiếp (O;R) đường kính BD ⇒ $\widehat{BCD}$  = 90° ⇒ DC ⊥ BC

⇒ CD // OA ( cùng vuông góc với BC) 

c) DC // OA ⇒ CE // OA ⇒ OCEA là hình thang

Có: $\widehat{OED}=\widehat{DBC}$  (cùng phụ với $\widehat{BDC}$ )

Mà: $\widehat{BAO}=\widehat{DBC}$  (cùng phụ với $\widehat{BOA}$  )

Nên: $\widehat{OED}=\widehat{BAO}$

Xét ΔODE và Δ BOA có:

$\widehat{DOE}=\widehat{OBA}$= 90°

OB = OD

$\widehat{OED}=\widehat{BAO}$

⇒ ΔODE = Δ BOA (g–c–g)

⇒ OE = AB ⇒ OE = AC

⇒ OCEA là hình thang cân (đpcm).