Cho đường tròn (O; R) và một điểm A ở ngoài đường tròn. Vẽ các tiếp tuyến AB
Cho đường tròn (O; R) và một điểm A ở ngoài đường tròn. Vẽ các tiếp tuyến AB, AC. Chứng minh rằng \(\widehat {BAC} = 60^\circ \) khi và chỉ khi OA = 2R
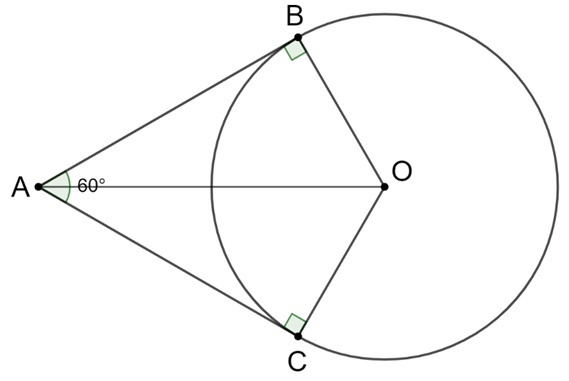
Xét ∆OAB và ∆OAC có:
OA: cạnh chung
OB = OC (bán kính của đường tròn (O))
\(\widehat {OBA} = \widehat {OCA} = 90^\circ \)
Þ ∆OAB = ∆OAC (cạnh huyền - cạnh góc vuông)
\( \Rightarrow \widehat {BAO} = \widehat {CAO} = \frac{{\widehat {BAC}}}{2} = 30^\circ \)
Xét tam giác vuông ACO:
\(\sin \widehat {CAO} = \frac{{OC}}{{OA}} \Leftrightarrow \sin 30^\circ = \frac{{OC}}{{OA}}\)
\( \Leftrightarrow OA = 2OC = 2R\)