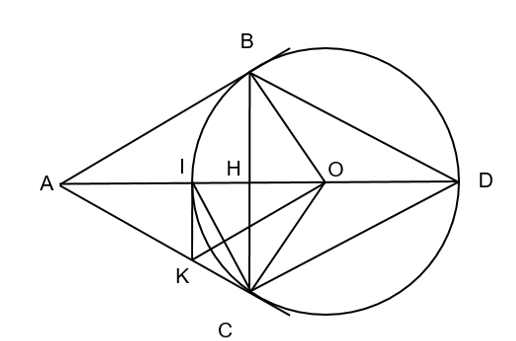
Cho đường tròn (O;R), và điểm A nằm ngoài đường tròn (O) sao cho OA = 2R.Vẽ tiếp tuyến AB với đường tròn (O). Gọi BH là đường cao của Δ ABO, BH cắt đường tròn (O) tại C.

a) Xét ∆OBC có OB = OC = R

Suy ra ∆OBC cân tại O có OH là đường cao nên OH cũng là phân giác.

Do đó $\widehat{AOB}=\widehat{AOC}$ .

Xét ∆BAO và ∆CAO có:

OB = OC = R

 $\widehat{AOB}=\widehat{AOC}$(cmt)

OA là cạnh chung

Do đó ∆BAO = ∆CAO (c.g.c)

$\widehat{ABD}=\widehat{ACD}={90}^o$ hay OC vuông góc với AC tại C.

Vậy AC là tiếp tuyến của (O).