Lời giải
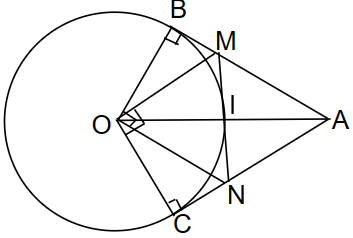
a) ) Xét (O; R) có AB là 2 tiếp tuyến tại điểm B
Suy ra AB ⊥ OB
Mà ON ⊥ OB
Nên AB // ON
Xét (O;R) có AB , AC là 2 tiếp tuyến cắt nhau tại A
Suy ra AB = AC và AO là tia phân giác của góc BAC
Xét (O; R) có AC là 2 tiếp tuyến tại điểm C
Suy ra AC ⊥ OC
Mà OM ⊥ OC
Nên AC // OM
Xét tứ giác AMON có AM // ON và AN // OM (chứng minh trên)
Suy ra AMON là hình bình hành
Mà AO là tia phân giác của góc MAN
Suy ra AMON là hình thoi
b) Gọi I là trung điểm của OA
Suy ra \[IA = IO = \frac{1}{2}OA = \frac{{2R}}{2} = R\].
Do đó OI là bán kính của (O)
Mà AMON là hình thoi
Nên OA vuông góc MN tại điểm I
Hay OI vuông góc MN tại điểm I
Xét (O; R) có OI là bán kính của (O), OI vuông góc MN tại điểm I
Suy ra MN là tiếp tuyến của đường tròn (O)
c) Vì AMON là hình thoi, AO cắt MN tại I
Nên I là trung điểm của MN
suy ra MN = 2 IN
Xét tam giác OAB vuông ở B có sin\(\widehat {OAB} = \frac{{OB}}{{AO}} = \frac{R}{{2{\rm{R}}}} = \frac{1}{2}\)
Suy ra \(\widehat {OAB}\) = 30°
Vì AB // ON nên \(\widehat {OAB} = \widehat {ION}\) (hai góc so le trong)
Mà \(\widehat {OAB}\) = 30°
Suy ra \(\widehat {ION} = 30^\circ \)
Xét tam giác OIN vuông ở I có \(\tan \widehat {ION} = \frac{{IN}}{{OI}}\)
Hay \(\tan 30^\circ = \frac{{IN}}{R}\)
Suy ra \(IN = \frac{R}{{\sqrt 3 }}\)
Mà MN = 2IN (chứng minh trên)
Do đó \(MN = \frac{{2R}}{{\sqrt 3 }}\)
Diện tích hình thoi AMON bằng: \(\frac{1}{2}OA.MN = \frac{1}{2}.2R.\frac{{2R}}{{\sqrt 3 }} = \frac{{2{R^2}}}{{\sqrt 3 }}\).
Vậy diện tích hình thôi AMON là \(\frac{{2{R^2}}}{{\sqrt 3 }}\).
