Cho đường tròn (O; R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thảng vuông góc với B tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.

a) Chứng minh: AMON là hình thoi.

b) Chứng minh: MN là tiếp tuyến của đường tròn.

c) Tính diện tích AMON.

Lời giải

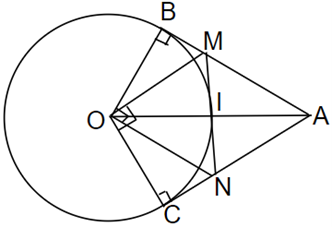
a) Do AB là tiếp tuyến của (O) Þ OB ^ AB

Mà OB ^ ON (gt) Þ AB // ON hay AM // ON (1)

Do AC là tiếp tuyến của (O) Þ OC ^ AC

Mà OC ^ OM (gt) Þ AC // OM hay AN // OM (2)

Từ (1) và (2) nên suy ra AMON là hình thoi

b) Đặt I là trung điểm của OA \( \Rightarrow OI = \frac{{OA}}{2} = \frac{{2R}}{2} = R\)

Hay OI là bán kính của (O).

Do AMON là hình thoi nên suy ra OA ^ MN tại I.

Hay OI ^ MN tại I.

Mà OI là bán kính của (O) Þ MN là tiếp tuyến của (O).

c) Xét tam giác OAB có OA ^ AB.

\( \Rightarrow \sin \widehat {OAB} = \frac{{OB}}{{AB}} = \frac{1}{2} \Rightarrow \widehat {OAB} = 30^\circ \)

\( \Rightarrow \widehat {ION} = 30^\circ \) (Hai góc ở vị trí so le trong).

Xét hình thoi AMON có OA cắt MN tại I Þ I là trung điểm MN.

Hay IN = IM = \(\frac{{MN}}{2}\).

Xét tam giác ION có \(\widehat {OIN} = 90^\circ ;\;\widehat {ION} = 30^\circ \)

\( \Rightarrow OI = IN.\cos \widehat {ION} = \frac{{MN}}{2}.\cos 30^\circ \)

\( \Rightarrow MN = \frac{{4.OI}}{{\sqrt 3 }} = \frac{{4R}}{{\sqrt 3 }}\).

\({S_{AMON}} = \frac{1}{2}OA.MN = \frac{1}{2}.2R.\frac{{4R}}{{\sqrt 3 }} = \frac{{4{R^2}}}{{\sqrt 3 }}\).