Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I.

a) Chứng minh: CO ⊥ AD.

b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE.CB = CI.CO.

c) Chứng minh: Trực tâm H của tam giác CAD di động trên đường cố định khi điểm C di chuyển trên Ax.

Lời giải

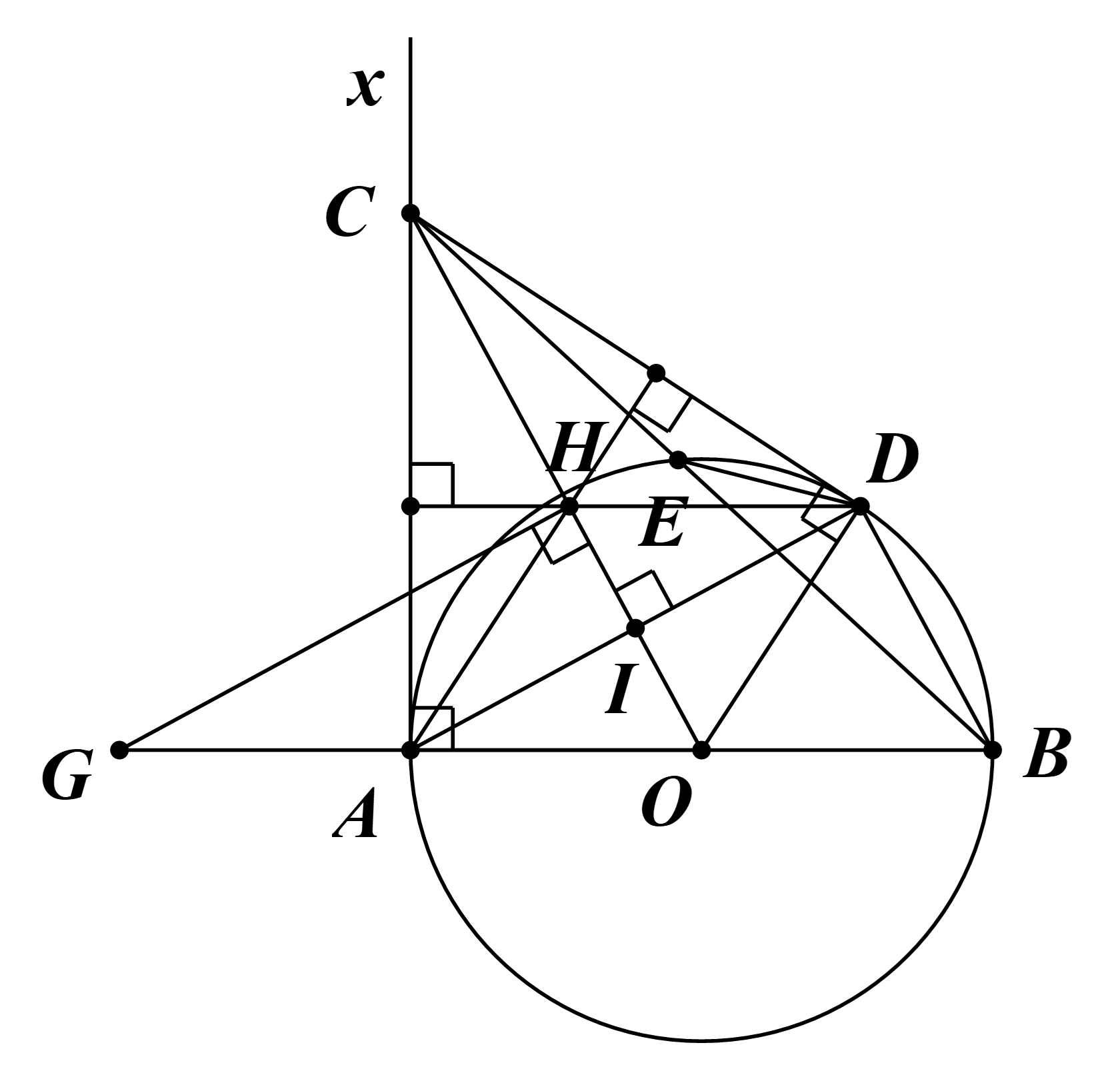
a) Ta có CA, CD là hai tiếp tuyến của (O) cắt nhau tại C.

Suy ra CA = CD.

Khi đó C nằm trên đường trung trực của đoạn thẳng AD   (1)

Lại có OA = OD = R.

Suy ra O nằm trên đường trung trực của đoạn thẳng AD   (2)

Từ (1), (2), suy ra CO là đường trung trực của đoạn thẳng AD.

Do đó CO ⊥ AD tại I.

b) Xét ∆CED và ∆CDB, có:

$\widehat C$ chung.

$\widehat {CDE} = \widehat {CBD}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung).

Do đó  (g.g).

Suy ra $\frac{{CE}}{{CD}} = \frac{{CD}}{{CB}}$.

Do đó CE.CB = CD²   (3)

Xét ∆CDO vuông tại D có DI là đường cao:

CD² = CI.CO (hệ thức lượng trong tam giác vuông)    (4)

Từ (3), (4), suy ra CE.CB = CI.CO (điều phải chứng minh).

c) Ta có AH // OD (cùng vuông góc với CD) và DH // OA (cùng vuông góc với AC).

Suy ra tứ giác AHDO là hình bình hành.

Mà I là giao điểm của AD và HO.

Do đó I là trung điểm của HO.

Trên tia đối của tia AO, lấy điểm G sao cho A là trung điểm của GO.

Khi đó AI là đường trung bình của tam giác GHO.

Suy ra AI // GH.

Mà AI ⊥ HO (chứng minh trên).

Do đó GH ⊥ HO.

Suy ra $\widehat {GHO} = 90^\circ$.

Vậy khi C di chuyển trên Ax thì trực tâm H của tam giác ACD di động trên đường tròn tâm A, bán kính AO cố định.