Cho đường tròn (O; R), đường kính AB. Trên đường tròn (O) lấy điểm D sao cho
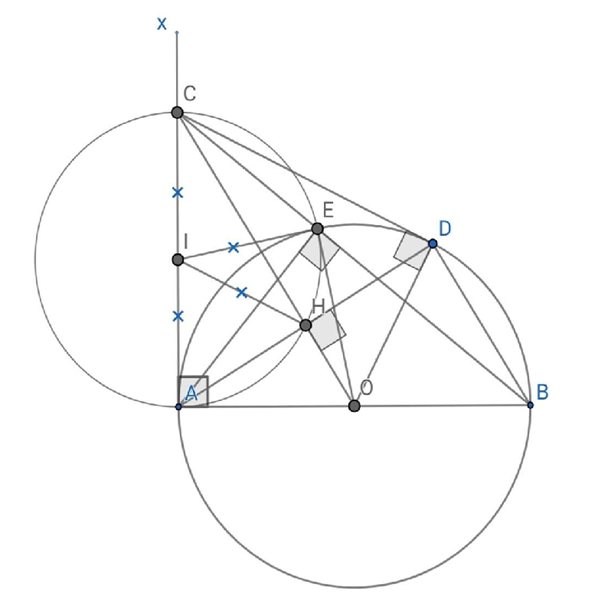
Cho đường tròn (O; R), đường kính AB. Trên đường tròn (O) lấy điểm D sao cho AD > BD, D khác A và B. Kẻ OH vuông góc với AD tại H, tia OH cắt tiếp tuyến Ax của đường tròn (O) tại C.
a) Chứng minh H là trung điểm của AD và OH.OC = R².
b) Gọi E là giao điểm của BC và đưởng tròn (O). Chứng minh bốn điểm A, H, E, C cùng thuộc một đường tròn và CD là tiếp tuyến của đường tròn (O).