Lời giải
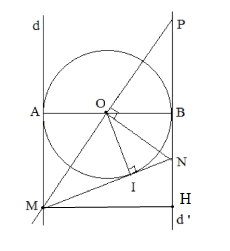
a) Vì (d) và (d’) là tiếp tuyến của (O) tại A, B
Nên OA ⊥ d, OB ⊥ d’
Suy ra ^OAM=90∘, ^OBP=90∘
Ta có đường tròn (O; R), đường kính AB
Nên OA = OB = R
Xét tam giác OAM và tam giác OBP có
^OAM=^OBP(=90∘)
OA = OB
^MOA=^POB (hai góc đối đỉnh)
Do đó △OAM = △OBP (g.c.g)
Suy ra OM = OP (hai cạnh tương ứng)
Xét tam giác MNP có NO vừa là đường cao vừa là đường trung tuyến
Suy ra tam giác MNP cân tại N
b) Xét tam giác MNP cân tại N có NO là đường cao
Suy ra NO là tia phân giác của góc MNP
Suy ra ^ONI=^ONB
Xét tam giác ONI và tam giác ONB có
^OIN=^OBN(=90∘)
ON là cạnh chung
^ONI=^ONB(chứng minh trên)
Do đó △ONI = △ONB (cạnh huyền – góc nhọn)
Suy ra OI = OB (hai cạnh tương ứng)
Mà OB = R nên OI = R
Xét (O; R) có OI = R, OI ⊥ MN
Suy ra MN là tiếp tuyến của (O) tại I
c) Xét (O) có MA , MI là hai tiếp tuyến cắt nhau tại M
Suy ra MA = MI
Xét (O) có NB , NI là hai tiếp tuyến cắt nhau tại N
Suy ra NB = NI
Vì tam giác OMN vuông tại O có OI ⊥ MN
Nên IM . IN = OI2 = R2
Mà MA = MI, NB = NI (chứng minh trên)
Suy ra AM . BN = R2
d) Tứ giác ABNM có ^MAB=^ABN=90∘
Nên ABNM là hình thang vuông
Suy ra SABNM=(AM+BN).AB2=(AI+IN).2R2=MN.R
Kẻ MH vuông góc d’
Ta có tam giác MHN vuông tại H
Suy ra MN ≥ MH
Để diện tích tứ giác ABNM nhỏ nhất
⟺ MN nhỏ nhất
Mà MN ≥ MH (chứng minh trên)
Dấu “ = ” xảy ra khi M ≡ H
Vậy điểm M nằm trên đường thẳng song song AB cách AB một khoảng bằng R thì diện tích tứ giác ABNM nhỏ nhất.

