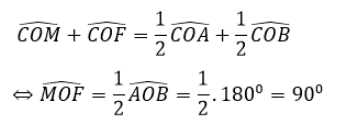Lời giải
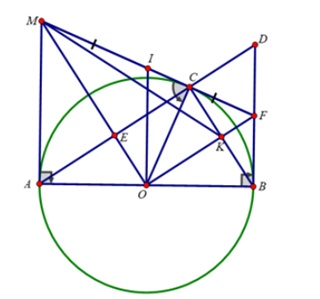
a) Xét (O) có MA, MC là hai tiếp tuyến cắt nhau tại M
Suy ra MA = MC
Hay M thuộc trung trực của AC (1)
Vì A, D cùng thuộc (O) nên OA = OD
Suy ra O thuộc đường trung trực của AC (2)
Từ (1) và (2) suy ra MO ⊥ AC
Suy ra ^OEC=90∘
Vì BD là tiếp tuyến của (O) nên BD ⊥ BO
Suy ra ^OBD=90∘
Xét tứ giác OBDE có ^OED+^OBD=90∘+90∘=180∘
Suy ra tứ giác OBDE nội tiếp
Vậy tứ giác OBDE nội tiếp
b) Vì tam giác ABC nội tiếp (O) đường kính AB
Nên tam giác ABC vuông tại C
Suy ra AC ⊥ BC
Xét tam giác ABD vuông tại B có BC ⊥ AD
Suy ra AC. AD = AB2 (hệ thức lượng trong tam giác vuông)
Mà AB = 2R
Suy ra AC . AD = 4R2
Vậy AC . AD = 4R2
c) Xét (O) có MA, MC là hai tiếp tuyến cắt nhau tại M
Suy ra OM là phân giác của góc AOC, MO là phân giác của góc AMC
Do đó ^COM=12^COA, ^OMA=^CMO
Xét (O) có FC, FB là hai tiếp tuyến cắt nhau tại F
Suy ra OF là phân giác của góc BOC
Do đó ^COF=12^COB
Khi đó :
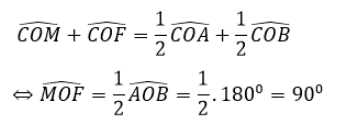
Suy ra tam giác MFO vuông tại O
Do đó tâm đường tròn ngoại tiếp tam giác MOF là trung điểm I của MF
Xét tam giác MFO vuông tại O có OI là trung tuyến
Suy ra IO = IM = IF
Do đó tam giác IMO cân tại I
Suy ra ^IOM=^IMO
Mà ^AMO=^IMO (chứng minh câu trên)
Suy ra ^AMO=^IOM
Vì tam giác AMO vuông tại A nên ^AMO+^AOM=90∘ (trong tam giác vuông tổng hai góc nhọn bằng 90°)
Hay ^MOI+^AOM=90∘
Suy ra ^AOI=90∘
Do đó AO ⊥ OI
Xét (I; IO) có AB ⊥ OI
Suy ra AB là tiếp tuyến
Vậy AB là tiếp tuyến của đường tròn ngoại tiếp tam giác MOF.