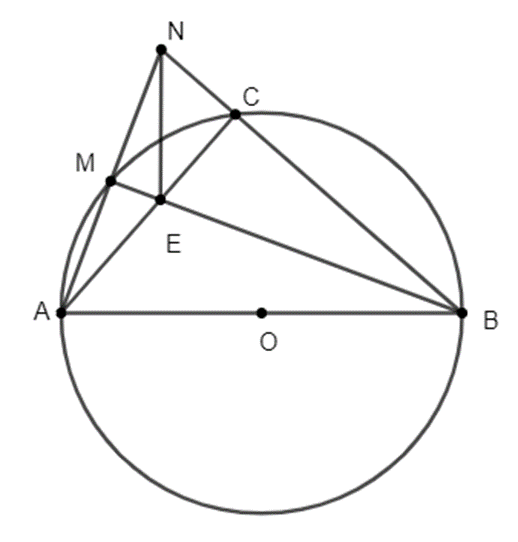
Cho đường tròn (O; R) có đường kính AB và điểm M thuộc đường tròn sao cho MA < MB (M khác A,B). Trên tia đối của tia MA lấy điểm N sao cho MN = MA. NB cắt (O) tại C, AC cắt BM tại E. Chứng minh: EM.EB = EC.EN.
Vì AB là đường kính của (O) nên ta có:
\(\widehat {AMB} = \widehat {ACB} = 90^\circ \)
\( \Rightarrow \)MB\( \bot \)AN, AC \( \bot \)BN.
Xét \(\Delta \)NEA có EM\( \bot \)AN
Mà AM là trung tuyến của \(\Delta AME\)
Suy ra EM đồng thời cũng là đường phân giác:
\(\widehat {MEN} = \widehat {MEA}\).
MÀ \(\widehat {MEA} = \widehat {CEB}\) (đối đỉnh)
\( \Rightarrow \widehat {MEN} = \widehat {CEB}\)
Xét \(\Delta MEN\) và \(\Delta BEC\) có:
\(\widehat {ECB} = \widehat {NME}\,\,( = 90^\circ )\)
\(\widehat {CEB} = \widehat {NEM}\)
\( \Rightarrow \Delta ECB\) ᔕ\(\Delta EMN\)(g.g)
\( \Rightarrow \frac{{EC}}{{EM}} = \frac{{EB}}{{EN}}\)
\( \Rightarrow \) EM.EB = EC.EN (đpcm)