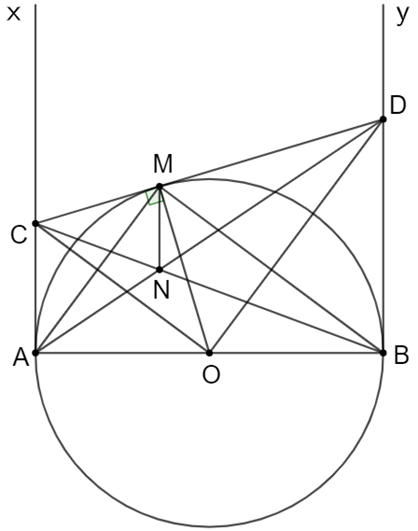
Cho đường tròn (O), đường kính AB, vẽ các tiếp tuyến Ax, By. Từ M trên đường tròn (M khác A,B) vẽ tiếp tuyến thứ ba nó cắt Ax ở C cắt By ở D.
Cho đường tròn (O), đường kính AB, vẽ các tiếp tuyến Ax, By. Từ M trên đường tròn (M khác A,B) vẽ tiếp tuyến thứ ba nó cắt Ax ở C cắt By ở D. Gọi N là giao điểm của BC và AD.
a) CMR: