Cho đường tròn (O) đường kính AB. Trên tiếp tuyến tại A của (O), lấy điểm C
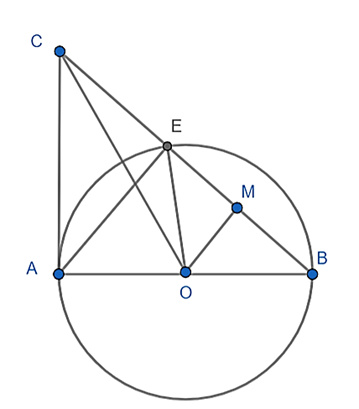
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến tại A của (O), lấy điểm C. Gọi E là giao điểm của CB với (O). từ O kẻ đường thẳng song song với AE cắt BC tại M.
a) Chứng minh CA2 = CE. CB
b) Chứng minh bốn điểm A; C; O; M cùng thuộc 1 đường tròn