Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ đường kính CD. Tia phân giác của góc BOD cắt AB tại E. a) Chứng minh rằng ED là tiếp tuyến củ
58
22/05/2024
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ đường kính CD. Tia phân giác của góc BOD cắt AB tại E.
a) Chứng minh rằng ED là tiếp tuyến của đường tròn (O).
b) Chứng minh AC + DE ≥ 2R.
c) Tính số đo góc AOE.
Trả lời
Lời giải
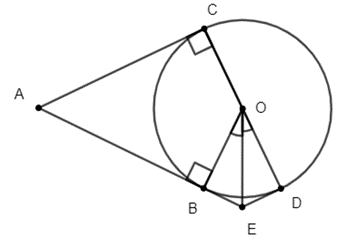
a) Xét ∆OBE và ∆ODE có:
OE là cạnh chung
\(\widehat {BOE} = \widehat {DOE}\) (giả thiết)
OB = OD (bán kính).
Do đó ∆OBE = ∆ODE (c.g.c).
Suy ra \(\widehat {OBE} = \widehat {ODE}\) (hai góc tương ứng).
Ta có \(\widehat {OBE} = 90^\circ \) (tính chất của tiếp tuyến) nên \(\widehat {ODE} = 90^\circ \).
Đường thẳng ED đi qua điểm D của đường tròn (O) và ED ⊥ OD nên ED là tiếp tuyến của đường tròn (O).
b) Theo tính chất của hai tiếp tuyến cắt nhau, ta có: AC = AB, DE = BE nên
AC + DE = AB + BE = AE (1)
Từ câu a) ta có CD ⊥ DE.
Mà CD ⊥ AC (giả thiết) nên ED // AC.
Ta có CD là khoảng cách giữa hai đường thẳng song song AC và DE
Do đó AE ≥ CD = 2R (2)
Từ (1) và (2) suy ra AC + DE ≥ 2R.
c) Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
OA là tia phân giác của \(\widehat {BOC}\), OE là tia phân giác của \(\widehat {BOD}\).
Mà \(\widehat {BOC},\,\,\widehat {BOD}\) là hai góc kề bù nên \(\widehat {AOE} = \widehat {BOC} + \widehat {BOD} = 90^\circ \).
Vậy \(\widehat {AOE} = 90^\circ \).

