Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). a) Chứng minh rằng: OA ⊥ BC. b) Vẽ đường kính CD. Chứng minh rằng BD so
34
12/05/2024
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng: OA ⊥ BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của ∆ ABC; Biết OB = 2 cm, OA = 4 cm.
Trả lời
Lời giải
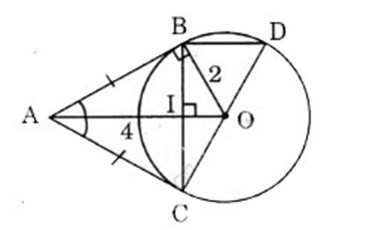
a) Vì AB, AC là các tiếp tuyến của (O) nên AB = AC nên ΔABC cân tại A.
Ta có AO là đường phân giác của góc \[\widehat {BAC}\] của tam giác cân ABC nên AO cũng là đường cao.
Suy ra OA ⊥ BC (tính chất của tam giác cân).
b) Gọi I là giao điểm của AO với BC.
Ta có ΔIBA = ΔICA (cạnh huyền - góc nhọn).
Suy ra IB = IC (hai cạnh tương ứng).
Trong ΔBCD có: IB = ID; OC = OD.
Suy ra OI là đường trung bình của ΔBCD.
Nên OI // BD hay AO// BD.
Vậy AO // BD (đpcm).
c) Vì AB là tiếp tuyến của (O) với B là tiếp điểm nên AB ⊥ OB và AB = AC.
Do đó ΔOAB vuông tại B.
Áp dụng định lí Py-ta-go vào tam giác vuông OAB, ta có:
AO2 = AB2 + BO2
⇒ AB2 = AO2 – BO2 = 42 – 22 = 12
⇒ AB = \[\sqrt {12} \] = \[2\sqrt 3 \] (cm)
Trong tam giác vuông OAB ta có
sin\[\widehat {OAB}\] = \[\frac{{OA}}{{OB}}\] = \[\frac{2}{4}\] = \[\frac{1}{2}\]
⇒ \[\widehat {OAB}\] = 30° ⇒ \[\widehat {BAC}\] = 2\[\widehat {OAB}\] = 2 . 30° = 60°
Xét ∆ABC cân tại A có \[\widehat A = 60^\circ \] nên ΔABC là tam giác đều.
Do đó AB = BC = CA = \[2\sqrt 3 \] (cm).

