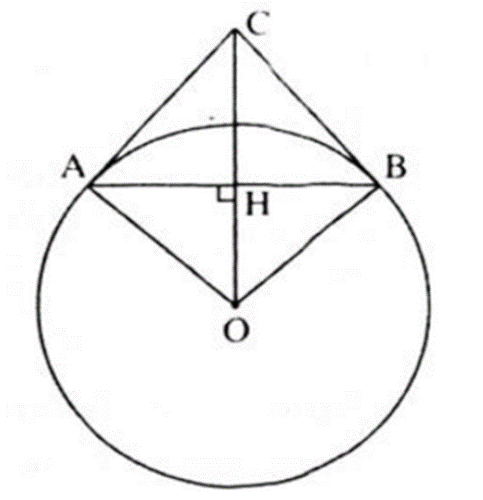
Gọi H là giao điểm của OC và AB

Vì OA = OB nên ΔAOB cân tại O

Mà OH là đường cao nên cũng là đường phân giác

Do đó $\widehat {AOC} = \widehat {BOC}$

Vì AC là tiếp tuyến tại A của đường tròn (O) nên $\widehat {OAC} = 90^\circ$

Xét ΔAOC và ΔBOC có

OA = OB

$\widehat {AOC} = \widehat {BOC}$ (chứng minh trên)

OC là cạnh chung

Do đó ΔAOC = ΔBOC (c.g.c)

Suy ra $\widehat {OAC} = \widehat {OBC}$ (hai góc tương ứng)

Mà $\widehat {OAC} = 90^\circ$ nên $\widehat {OBC} = 90^\circ$

Suy ra CB vuông góc với OB, mà OB là bán kính của đường tròn (O)

Do đó CB là tiếp tuyến của đường tròn (O) tại B

Vậy CB là tiếp tuyến của đường tròn (O) tại B.