Lời giải
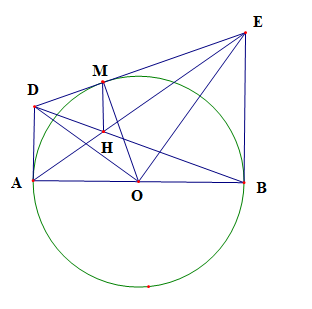
a) Xét (O) có DM, DA là hai tiếp tuyến cắt nhau tại D
Suy ra DA = DM
Xét (O) có EM, EB là hai tiếp tuyến cắt nhau tại E
Suy ra EB = EM
Ta có DE = DM + ME = DA + EB
Vậy DE = AD + BE.
b) Xét (O) có DM, DA là hai tiếp tuyến cắt nhau tại D
Suy ra OD là tia phân giác của góc AOM
Do đó \(\widehat {AO{\rm{D}}} = \widehat {MO{\rm{D}}} = \frac{1}{2}\widehat {AOM}\)
Xét (O) có EM, EB là hai tiếp tuyến cắt nhau tại E
Suy ra OE là tia phân giác của góc BOM
Do đó \(\widehat {BOE} = \widehat {EO{\rm{D}}} = \frac{1}{2}\widehat {BOM}\)
Ta có \(\widehat {AOM} + \widehat {BOM} = 180^\circ \) (hai góc kề bù)
Suy ra \(\frac{1}{2}\widehat {AOM} + \frac{1}{2}\widehat {BOM} = 90^\circ \)
Hay \(\widehat {DOM} + \widehat {EOM} = 90^\circ \)
Suy ra \(\widehat {DOE} = 90^\circ \)
Suy ra tam giác DOE vuông tại O
Vậy tam giác DOE vuông tại O.
c) Ta có AD ⊥ AB, EB ⊥ AB
suy ra AD // EB
Xét tam giác AHD có AD // EB
Nên \(\frac{{DH}}{{HB}} = \frac{{DA}}{{BE}}\)
Mà DA = DM, EB = EM
Suy ra \(\frac{{DH}}{{HB}} = \frac{{DM}}{{ME}}\)
Do đó MH // BE
Lại có EB ⊥ AB
Suy ra MH ⊥ AB
Vậy MH ⊥ AB.

