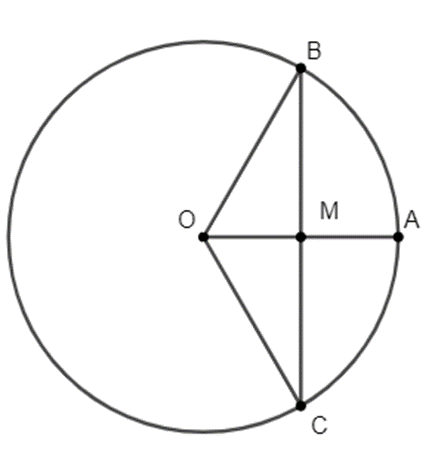
Vì B, C thuộc đường tròn (O) nên: OB = OA = OC = 4 cm.

M là trung điểm của OA

\( \Rightarrow OM = \frac{1}{2}OA = 2\) (cm)

Xét \(\Delta OBC\) có OB = OC suy ra \(\Delta OBC\) cân tại O.

Suy ra OM là đường cao đồng thời là trung tuyến nên ta có:

MB = MC \( \Rightarrow MB = \frac{1}{2}BC\)

Xét \(\Delta OBM\) có \(\widehat M = 90^\circ \)

\( \Rightarrow \) OB² = OM² + MB²

\( \Rightarrow MB = \sqrt {O{B^2} - O{M^2}} = \sqrt {{4^2} - {2^2}} = 2\sqrt 3 \) (cm)

\( \Rightarrow BC = 2MB = 4\sqrt 3 \) (cm).