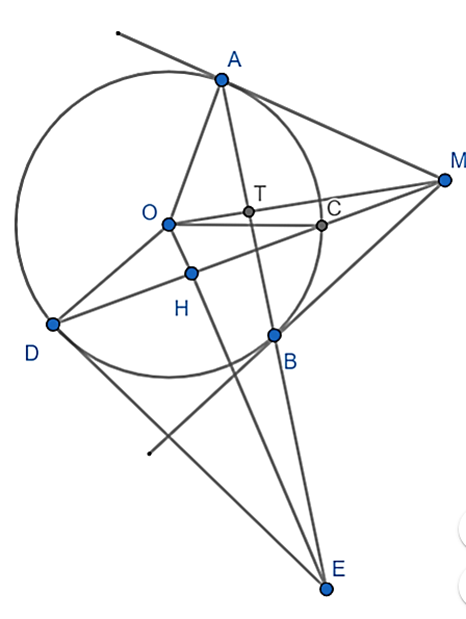
Cho đường thẳng d cắt đường tròn (O;R) tại 2 điểm C, D. M là 1 điểm thuộc d và nằm ngoài (O;R) (MC < MD). Vẽ 2 tiếp tuyến MA, MB với (O;R). H là trung điểm của CD. Đường thẳng AB cắt OH tại E. Chứng minh ED là tiếp tuyến của (O; R).
Ta có: MA, MB là tiếp tuyến của (O)
Nên MA = MB và MO là phân giác \(\widehat {AMB}\)
Suy ra: MO vuông góc AB
Gọi H là trung điểm DC; T là giao điểm AE và OM
Suy ra: OH vuông góc DC. OT vuông góc AB (tính chất)
Xét tam giác OHM và tam giác OTE có:
Chung \(\widehat O\)
\(\widehat {OTE} = \widehat {OHM} = 90^\circ \)
⇒ ∆OTE ∽ ∆OHM (g.g)
⇒ \(\frac{{OH}}{{OT}} = \frac{{OM}}{{OE}}\)
⇒ OH.OE = OM.OT
Tam giác AOM vuông tại A có AT là đường cao nên OA2 = OT.OM
Mà OA = OD nên OD2 = OT.OM = OH.OE
⇒ \(\frac{{OD}}{{OH}} = \frac{{OE}}{{OD}}\)
Xét ∆ODH và ∆OED có:
\(\frac{{OD}}{{OH}} = \frac{{OE}}{{OD}}\)
\(\widehat {DOH}\)chung
⇒ ∆ODH ∽ ∆OED (g.g)
⇒ \(\widehat {ODE} = \widehat {OHD} = 90^\circ \)
⇒ OD vuông góc ED tại D
Vậy ED là tiếp tuyến (O).