Cho đồ thị hàm số y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của
Cho đồ thị hàm số y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình \(f(x) = \frac{1}{2}\) là:
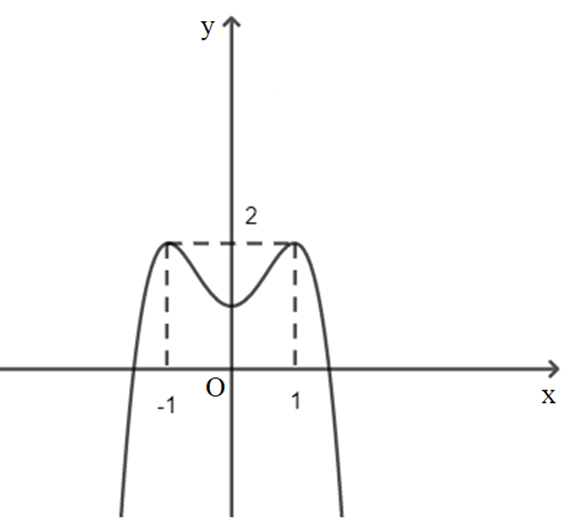
A. 2;
B. 4;
C. 1;
D. 3.
Cho đồ thị hàm số y = f(x) có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình \(f(x) = \frac{1}{2}\) là:

A. 2;
B. 4;
C. 1;
D. 3.
Đáp án đúng là: A
Số nghiệm thực của phương trình \(f(x) = \frac{1}{2}\) chính là số giao điểm của đồ thị hàm số f(x) với đường thẳng \(y = \frac{1}{2}\).
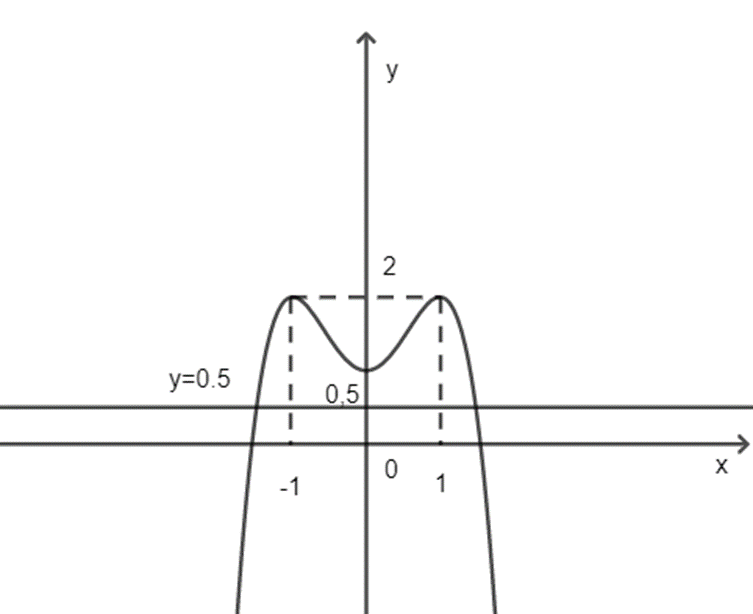
Dựa vào hình trên ta thấy đồ thị hàm số f(x) với đường thẳng \(y = \frac{1}{2}\) có hai giao điểm.
Vậy phương trình f(x) = \(\frac{1}{2}\) có hai nghiệm.