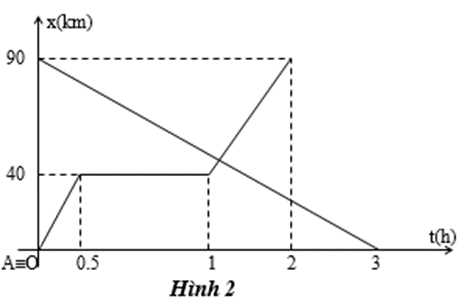
Cho đồ thị chuyển động của hai xe được mô tả trên hình vẽ.

a. Hãy nêu đặc điểm chuyển động của hai xe.

b. Tình thời điểm hai xe gặp nhau, lúc đó mỗi xe đi được quãng đường là bao nhiêu ?(Hình 2)

a, Xe 1 chia làm ba giai đoạn

Giai đoạn 1:

Ta có \({v_1} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} = \frac{{40 - 0}}{{0,5 - 0}} = 80\) km/h

Xe chuyển động theo chiều dương với 80 km/h xuất phát từ gốc tọa độ

Phương trình chuyển động:

\({x_{gd1}} = 80t\,\,\,\,\,\,\,\,\,\left( {0 \le t \le 0,5} \right)\)

Giai đoạn 2:

Ta có \({v_2} = \frac{{{x_3} - {x_4}}}{{{t_3} - {t_4}}} = \frac{{40 - 40}}{{1 - 0,5}} = 0\) km/h

Xe đứng yên tại vị trí cách gốc tọa độ là 40km trong khoảng thời gian 0,5h

 Phương trình chuyển động gđ 2: 

\({x_{gd2}} = 40 + 0\left( {t - 0,5} \right)\,\,\,\,\,\,\,\,\,\,\left( {0,5 \le t \le t} \right)\)

Giai đoạn 3

Ta có \({v_{gd3}} = \frac{{{x_5} - {x_4}}}{{{t_5} - {t_4}}} = \frac{{90 - 40}}{{2 - 1}} = 50\) km/h

Xe vẫn chuyển động theo chiều dương với 50 km/h xuất phát cách gốc tọa độ 40km và xuất phát sau gốc thời gian là 1h

Phương trình chuyển động:

\({x_3} = 40 + 50\left( {t - - 1} \right)\,\,\,\,\,\,\,\,\left( {1 \le t \le 2} \right)\)

Đới với xe 2:

Ta có \(v = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} = \frac{{0 - 90}}{{3 - 0}} = - 30\) km/h

Vậy xe 2 chuyển động theo chiều âm với vận tốc -30 km/h xuất phát cách gốc tọa độ là 90km, cùng gốc thời gian  

\({x_{x2}} = 90 - 30t\,\,\,\,\,\,\left( {0 \le t \le 3} \right)\)

b; Từ hình vẽ ta nhận thấy hai xe gặp nhau ở giai đoạn 3 của xe một

 Ta có:

\({x_{x2}} = {x_3} \Rightarrow 90 - 30t = 40 + 50\left( {t - 1} \right)\)

\( \Rightarrow t = \frac{5}{4}h = 1,25h\)

Vậy sau 1h15 phút hai xe gặp nhau và xe hai đi được quãng đường:

\({s_2} = vt = 30.1,25 = 37,5km\)

Xe một đi được quãng đường

\({s_1} = 90 - 37,5 = 52,5km\)