Cho điểm D nằm trong tam giác ABC sao cho góc DAB = góc DBC = góc DCA = phi. Chứng minh rằng: sin3φ = sin(A – φ). sin(B – φ). sin(C – φ).

Trả lời

Lời giải

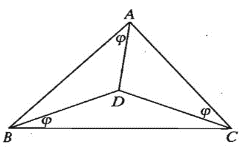
Theo định lý sin, trong tam giác ABD ta có:

\(\frac{{DB}}{{\sin \varphi }} = \frac{{AD}}{{\sin \left( {B - \varphi } \right)}}\)

Trong tam giác BCD có:

\(\frac{{CD}}{{\sin \varphi }} = \frac{{BD}}{{\sin \left( {C - \varphi } \right)}}\)

Trong tam giác ACD có:

\(\frac{{AD}}{{\sin \varphi }} = \frac{{CD}}{{\sin \left( {A - \varphi } \right)}}\)

Suy ra:

\(\frac{{B{\rm{D}}}}{{\sin \varphi }}.\frac{{C{\rm{D}}}}{{\sin \varphi }}.\frac{{A{\rm{D}}}}{{\sin \varphi }} = \frac{{AD}}{{\sin \left( {B - \varphi } \right)}}.\frac{{BD}}{{\sin \left( {C - \varphi } \right)}}.\frac{{CD}}{{\sin \left( {A - \varphi } \right)}}\)

Do đó: sin³φ = sin(A – φ). sin(B – φ). sin(C – φ)

Vậy sin³φ = sin(A – φ). sin(B – φ). sin(C – φ).