Cho các điểm A(1; – 2), B(– 2; 3) và C(0; 4). Diện tích tam giác ABC bằng bao nhiêu?

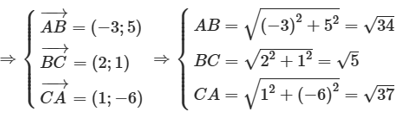
Nửa chu vi tam giác ABC là:

\(p = \frac{{AB + BC + CA}}{2} = \frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2}\)

Suy ra:

• \(p - AB = \frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2} - \sqrt {34} = \frac{{\sqrt 5 + \sqrt {37} - \sqrt {34} }}{2}\)

• \(p - BC = \frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2} - \sqrt 5 = \frac{{\sqrt {34} + \sqrt {37} - \sqrt 5 }}{2}\)

• \(p - CA = \frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2} - \sqrt {37} = \frac{{\sqrt 5 + \sqrt {34} - \sqrt {37} }}{2}\)

Diện tích tam giác ABC là:

\({S_{ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - BC} \right)\left( {p - CA} \right)} \)

\( = \sqrt {\frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2}.\left( {\frac{{\sqrt 5 + \sqrt {37} - \sqrt {34} }}{2}} \right).\left( {\frac{{\sqrt {34} + \sqrt {37} - \sqrt 5 }}{2}} \right).\left( {\frac{{\sqrt {34} + \sqrt 5 - \sqrt {37} }}{2}} \right)} \)

\( = \sqrt {\left( {\frac{{\sqrt {34} + \sqrt 5 + \sqrt {37} }}{2}} \right).\left( {\frac{{\sqrt {34} + \sqrt 5 - \sqrt {37} }}{2}} \right)\left( {\frac{{\sqrt {37} + \sqrt 5 - \sqrt {34} }}{2}} \right).\left[ {\frac{{\sqrt {37} - \left( {\sqrt 5 - \sqrt {34} } \right)}}{2}} \right]} \)

\[ = \frac{{\sqrt {\left[ {{{\left( {\sqrt {34} + \sqrt 5 } \right)}^2} - 37} \right].\left[ {37 - {{\left( {\sqrt 5 - \sqrt {34} } \right)}^2}} \right]} }}{4}\]

\[ = \frac{{\sqrt {\left[ {34 + 2\sqrt {170} + 5 - 37} \right].\left[ {37 - \left( {5 - 2\sqrt {170} + 34} \right)} \right]} }}{4}\]

\[ = \frac{{\sqrt {\left( {2 + 2\sqrt {170} } \right).\left( {2\sqrt {170} - 2} \right)} }}{4}\]

\[ = \frac{{\sqrt {4.170 - 4} }}{4} = \frac{{2.\sqrt {170 - 1} }}{4} = \frac{{\sqrt {169} }}{2} = \frac{{13}}{2}\]

Vậy diện tích tam giác ABC bằng \(\frac{{13}}{2}\).