Cho biểu thức $P = \left( {\frac{{2 + x}}{{2 - x}} - \frac{{4{{\rm{x}}^2}}}{{{x^2} - 4}} - \frac{{2 - x}}{{2 + x}}} \right):\frac{{{x^2} - 3{\rm{x}}}}{{2{{\rm{x}}^2} - {x^3}}}$.

a) Rút gọn P.

b) Tìm giá trị nguyên của x để P chia hết cho 4.

a) Điều kiện xác định x ≠ {– 2; 0; 2; 3}

Ta có $P = \left( {\frac{{2 + x}}{{2 - x}} - \frac{{4{{\rm{x}}^2}}}{{{x^2} - 4}} - \frac{{2 - x}}{{2 + x}}} \right):\frac{{{x^2} - 3{\rm{x}}}}{{2{{\rm{x}}^2} - {x^3}}}$

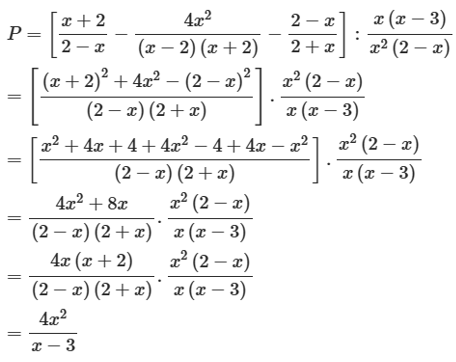
b) Với x ≠ {– 2; 0; 2; 3}, ta có

$P = \frac{{4{{\rm{x}}^2}}}{{x - 3}} = \frac{{4x(x - 3) + 12\left( {x - 3} \right) + 36}}{{x - 3}} = 4{\rm{x}} + 12 + \frac{{36}}{{x - 3}}$

$P:4 = x + 3 + \frac{9}{{x - 3}}$

Để P ⋮ 4 thì 9 ⋮ x – 3

Suy ra x – 3 ∈ Ư(9) = {1; 3; 9; – 1; – 3; – 9}

Do đó x ∈ {4; 6; 12; 2; 0; – 6}

Mà x ≠ {– 2; 0; 2; 3}

Suy ra x ∈ {4; 6; 12; – 6}

Vậy x ∈ {4; 6; 12; – 6}.