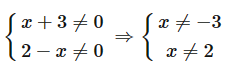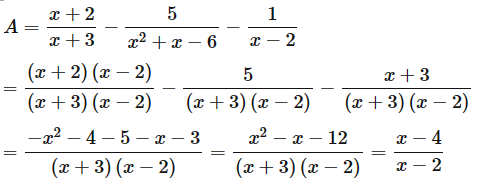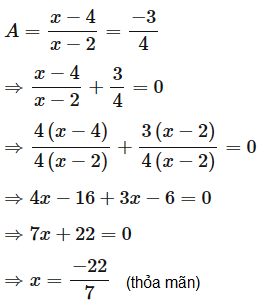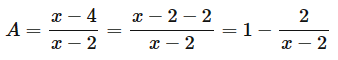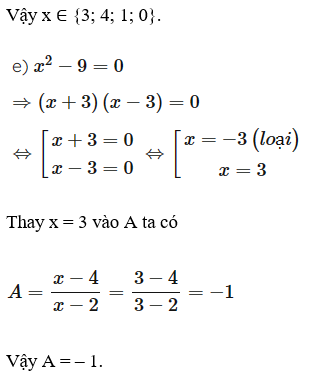Cho biểu thức \(A = \frac{{x + 2}}{{x + 3}} - \frac{5}{{{x^2} + x - 6}} + \frac{1}{{2 - x}}\).

a) Tìm điều kiện để A có nghĩa (xác định).

b) Rút gọn A.

c) Tìm x để \(A = \frac{{ - 3}}{4}\).

d) Tìm x để biểu thức A nguyên.

e) Tính giá trị của A khi x² – 9 = 0.

a) Điều kiện xác định của A là

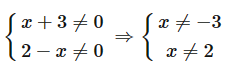
b) Với \(x \ne - 3;x \ne 2\) ta có

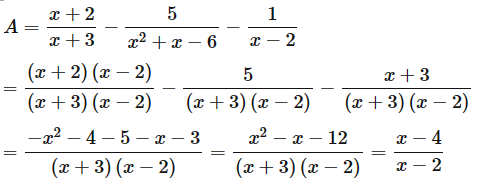
c) Với \(x \ne - 3;x \ne 2\), để \(A = \frac{{ - 3}}{4}\) thì

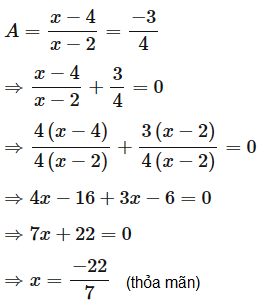
Vậy \(x = \frac{{ - 22}}{7}\) thì \(A = \frac{{ - 3}}{4}\).

d) Với \(x \ne - 3;x \ne 2\) ta có

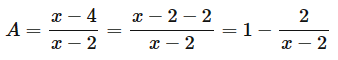
Để A nguyên thì \(\frac{2}{{x - 2}}\) nguyên

Suy ra x – 2 ∈ Ư(2) = {1; 2; – 1; – 2}

Suy ra x ∈ {3; 4; 1; 0} (thỏa mãn)

Vậy x ∈ {3; 4; 1; 0}.