Cho biết log25 7 = a và log2 5 = b. Tính log căn bậc ba 5 = 49/8 theo a, b
Cho biết log25 7 = a và log2 5 = b. Tính log3√5498 theo a, b.
A. 2(ba−3)b;
B. −4ba+3b;
C. b4ab+1;
D. 3(4ab−3)b.
Cho biết log25 7 = a và log2 5 = b. Tính log3√5498 theo a, b.
A. 2(ba−3)b;
B. −4ba+3b;
C. b4ab+1;
D. 3(4ab−3)b.
Đáp án đúng là: D
Ta có:
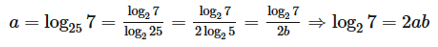
Do đó :
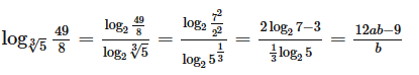
Vậy ta chọn đáp án D.