Cho ∆ABC vuông tại A vẽ đường cao AH có AB = 6 cm, AC = 8 cm.

a) Chứng minh ∆HBA ᔕ ∆ABC.

b) Tính BC, AH, HC.

c) Chứng minh AH² = HB . HC.

Lời giải

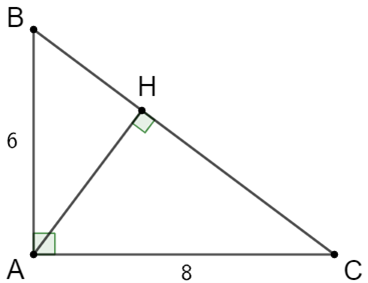
a) Xét ∆HBA và ∆ABC có:

$\widehat B$ chung

$\widehat {AHB} = \widehat {BAC} = 90^\circ$

Þ ∆HBA ᔕ ∆ABC (g.g).

b) Áp dụng định lí Py-ta-go với ∆ABC vuông tại A nên ta có:

BC² = AB² + AC²

Þ BC² = 6² + 8² = 100

Þ BC = 10 cm

∆HBA ᔕ ∆ABC

$\Rightarrow \frac{{HA}}{{AC}} = \frac{{AB}}{{CB}} \Rightarrow \frac{{AH}}{8} = \frac{6}{{10}} \Rightarrow AH = 4,8\;cm$.

Áp dụng định lí Pytago vào ∆AHC vuông tại H nên ta có:

$HC = \sqrt {A{C^2} - A{H^2}} = \sqrt {{8^2} - {{4,8}^2}} = 3,6\;(cm)$.

c) Xét ∆AHB và ∆CHA có:

$\widehat {AHB} = \widehat {CHA} = 90^\circ$

$\widehat {BAH} = \widehat {ACH}$ (cùng phụ với $\widehat {ABC}$)

Þ ∆AHB ᔕ ∆CHA (g.g)

$\Rightarrow \frac{{AH}}{{CH}} = \frac{{HB}}{{HA}} \Rightarrow A{H^2} = HB.HC$.