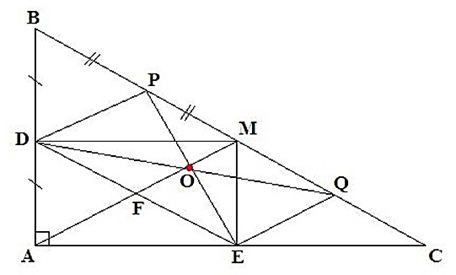
a) Ta có D, E là hình chiếu của M trên AB, AC

⇒ DM ⊥ AB và ME ⊥ AC Mà AB ⊥ AC.

⇒ ADME là hình chữ nhật.

b) Xét ΔABC có:

M là trung điểm BC và ME // AB (ADME là hình chữ nhật)

⇒ ME là đường trung bình của ΔABC ⇒ E là trung điểm AC

M là trung điểm BC và MD // AC (ADME là hình chữ nhật)

⇒ MD là đường trung bình của ΔABC ⇒ D là trung điểm AB

Ta có: E là trung điểm AC, D là trung điểm AB

⇒ DE là đường trung bình của ΔABC

⇒ DE = \(\frac{1}{2}\)BC.

c) Xét ΔBAM có D, P lần lượt là trung điểm của AB và BM

⇒ DP là đường trung bình của ΔBAM.

⇒ DP // AM (1)

Chứng minh tương tự với ΔAMC ⇒ EQ // AM (2)

Từ (1) và (2) ⇒ DP // EQ Mà DE // PQ (cmt)

⇒ DPQE là hình bình hành

Gọi O là tâm đối xứng của DPQE (là giao điểm 2 đường chéo)

Ta có P, Q là trung điểm của BM và MC và M là trung điểm BC

⇒ M là trung điểm PQ

Xét hình bình hành DPQE có AM // DP và M là trung điểm PQ

⇒ AM là đường trung bình của DPQE

⇒ AM đi qua trung điểm DE, gọi điểm đó là F

Từ đó AM là trục đối xứng của DPQE tức là đi qua O.

d) Để DPQE là hình chữ nhật thì 4 góc của hình phải bằng 90°

Ta xét ΔBAM nếu DP⊥BM thì AM⊥BM

Xét ΔABC có AM vừa là đường trung tuyến vừa là đường cao

⇒ ΔABC vuông cân tại A

⇒ AB = AC.