Cho ∆ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC.

a) Chứng minh rằng D đối xứng với E qua A.

b) Tam giác DHE là tam giác gì? Vì sao?

c) Tứ giác BDEC là hình gì? Vì sao?

d) Chứng minh rằng BC = BD + CE.

Lời giải

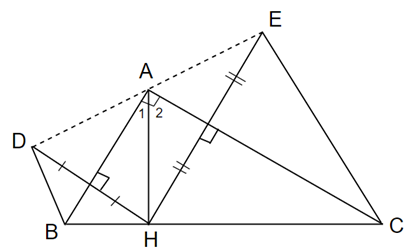
a) Vì D đối xứng với H qua AB nên AB là đường trung trực của DH 
nên AH = AD        (1) 
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE 
nên AH = AE         (2) 
Từ (1) và (2) ⇒ AD = AE (3) 

Mặt khác: $\widehat {DBA} = \widehat {BAH}$; $\widehat {HAC} = \widehat {CAE}$

$\widehat {BAH} = \widehat {HAC}$ = 90°
Do đó $\widehat {DAB} + \widehat {BAH} + \widehat {HAC} + \widehat {CAE}$ = 180° 
Tức là ba điểm D, A, E thẳng hàng      (4) 

Từ (3) và (4) suy ra D và E đối xứng với nhau qua A. 
b) ∆ DHE có HA là trung tuyến và $HA = \frac{1}{2}DE$ nên ∆DHE vuông tại H. 
c) Ta có: ∆ADB = ∆AHB (c.c.c) 
Suy ra $\widehat {ADB} = \widehat {AHB}$ = 90° 
Tương tự có $\widehat {AEC}$ = 90°
⇒ BD // CE (cùng vuông góc với DE) 
Nên tứ giác BAEC là hình thang có 2 góc vuông kề cạnh bên DE.

Do đó tứ giác BAEC là hình thang vuông. 
d) Do AB là đường trung trực của DH nên BD = BH          (5) 
Do AC là đường trung trực của EH nên CE = CH   (6) 
Cộng vế với vế của (5) và (6) ta suy ra BD + CE = BH + CH.
Hay BD + CE = BC.