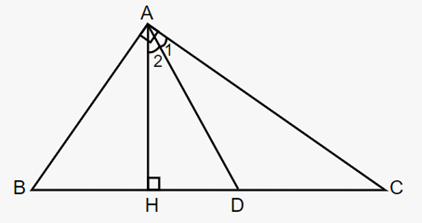
Cho ∆ABC vuông tại A, đường cao AH. Gọi AD là phân giác trong của ∆AHC. a) Chứng minh ∆ BAD là tam giác cân; b) Cho BC = 25 cm, HD = 6 cm. Tính AB.
36
12/05/2024
Cho ∆ABC vuông tại A, đường cao AH. Gọi AD là phân giác trong của ∆AHC.
a) Chứng minh ∆ BAD là tam giác cân;
b) Cho BC = 25 cm, HD = 6 cm. Tính AB.
Trả lời
Lời giải
a) Ta có \[\widehat {BDA} = 90^\circ - {\widehat A_2}\] ; \[{\widehat A_1} = {\widehat A_2}\].
Suy ra \[\widehat {BAD} = \widehat {BDA}\].
Do đó ∆BAD cân tại B.
b) Ta có BH . BC = AB2
⇒ (x – 6) . 25 = x2 ⇒ x2 − 25x + 150 = 0
⇔ x = 10 hoặc x = 15.
Vậy AB = 10 cm hoặc AB = 15 cm.
