Cho ∆ ABC vuông tại A có AB = 3 cm, AC = 4 cm. a) Giải ∆ABC. b) Gọi I là trung điểm của BC, vẽ AH ⊥ BC. Tính AH, AI. c) Qua A kẻ đường thẳng vuông góc với AI. Đường thẳng vuông góc với BC
28
12/05/2024
Cho ∆ ABC vuông tại A có AB = 3 cm, AC = 4 cm.
a) Giải ∆ABC.
b) Gọi I là trung điểm của BC, vẽ AH ⊥ BC. Tính AH, AI.
c) Qua A kẻ đường thẳng vuông góc với AI. Đường thẳng vuông góc với BC tại B cắt xy tại điểm M, đường thẳng vuông góc với BC tại C cắt xy tại điểm N. Chứng minh \[MB\,\,.\,NC = \frac{{B{C^2}}}{4}\].
Trả lời
Lời giải
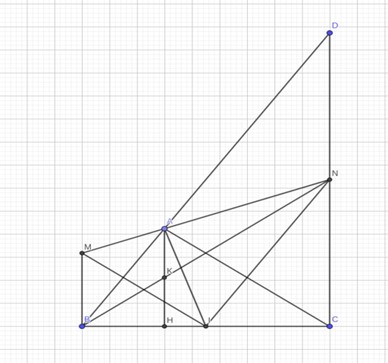
Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:
BC = \[\sqrt {A{B^2} + A{C^2}} = 5\] (cm)
sin\[\widehat B\] = \[\frac{{AB}}{{AC}} = \frac{4}{5}\] ⇒ \[\widehat B \approx 53^\circ \]
\[\widehat C = 90^\circ - \widehat B = 37^\circ \]
b) Vì AI là trung tuyến ứng ch BC nên AI = \[\frac{1}{2}\]BC = 2,5 (cm)
AH. BC = AB . AC ⇒ AH = \[\frac{{AB.AC}}{{BC}} = \frac{{12}}{5}\](cm)
c) Xét ∆AMI và ∆BMI có:
IA = IB
\[\widehat {IAM} = \widehat {IAM} = 90^\circ \]
IM chung
Do đó ∆AMI = ∆BMI (cạnh huyền – góc vuông)
Suy ra \[\left\{ \begin{array}{l}MA = MB\\\widehat {AIM} = \widehat {BIM}\end{array} \right.\] (các cạnh và các góc tương ứng).
Do đó IN là phân giác của \[\widehat {AIC}\].
Do \[\widehat {AIB} + \widehat {AIC}\]= 180° nên IM ⊥ IN.
Suy ra ∆IMN vuông tại I.
Mà IA ⊥ MN
Do đó MB . NC = AM . AN = IA2 = \[{\left( {\frac{{BC}}{2}} \right)^2} = \frac{{B{C^2}}}{4}\]

