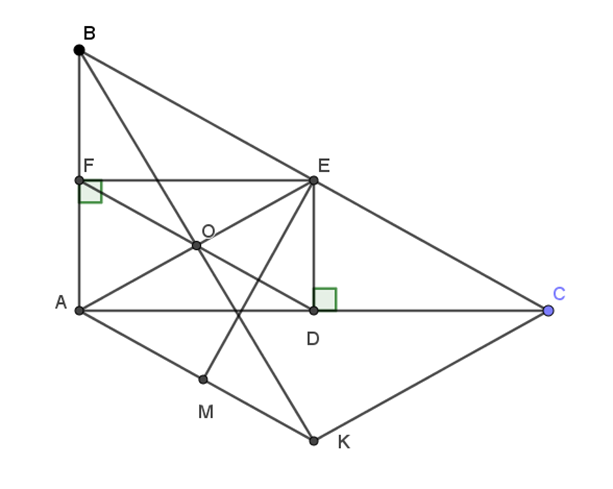
a)
EF vuông góc với AB do đó ^AFE=90∘
ED vuông góc với AC do đó ^ADE=90∘
Tứ giác ADEF có:
^FAD=90∘
^AFE=90∘
^ADE=90∘
Do đó, ADEF là hình chữ nhật
b)
K đối xứng với E qua D
Do đó D là trung điểm của EK
ED vuông góc với AC, AB vuông góc với AC
Do đó, ED song song với AB
Tam giác ABC có:
E là trung điểm của BC
ED song song với AB
Do đó, D là trung điểm của AC
Tứ giác AECK có:
D là trung điểm của AC, EK
Do đó, AECK là hình bình hành mà EK vuông góc với AC
Do đó, AECK là hình thoi
c)
ADEF là hình chữ nhật, DF và AE giao nhau tại O
Nên O là trung điểm của DF, AE và DF = AE
AECK là hình thoi nên AK = EC, AK song song với EC
AK = EC, BE = EC nên AK = BE
Tứ giác ABEK có:
AK = BE
AK song song với BE
Do đó, ABEK là hình bình hành
Do đó, AE, BK cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm của AE, O là trung điểm của BK
Do đó, B, O, K thẳng hàng
d)
Tam giác AME vuông tại M có MO là đường trung tuyến
MO=12AE=12DF
Tam giác FMD có:
MO=12DF
MO là đường trung tuyến
Do đó, FMD vuông tại M
⇒^DMF=90∘