Cho ∆ABC nhọn (AB < AC). Đường tròn tâm O, đường kính BC lần lượt cắt AB, AC tại M và N; BM và CN giao nhau tại H, AH cắt BC tại K. a) Chứng minh: AK ⊥ BC. b) Chứng minh: AM . AB = AN . AC.
43
12/05/2024
Cho ∆ABC nhọn (AB < AC). Đường tròn tâm O, đường kính BC lần lượt cắt AB, AC tại M và N; BM và CN giao nhau tại H, AH cắt BC tại K.
a) Chứng minh: AK ⊥ BC.
b) Chứng minh: AM . AB = AN . AC.
Trả lời
Lời giải
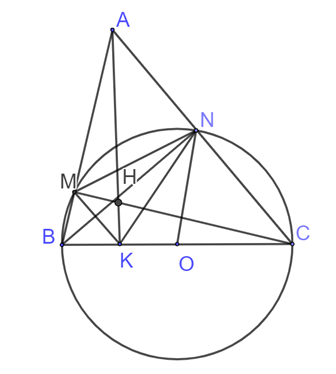
a) Do N ∈ (O) ⇒ \(ON = \frac{1}{2}BC\)⇒ BN ⊥ AC;
M ∈ (O) ⇒ \[MO = \frac{1}{2}BC\] ⇒ MC ⊥ AB.
⇒ H là giao điểm của đường cao
⇒ AH ⊥ BC
⇒ AK ⊥ BC.
b) Xét ∆ANB và ∆AMC có
\[\widehat {BAC}\]là góc chung
\[\widehat {ANB} = \widehat {AMC}\](= 90°)
Do đó ∆ANB ᔕ ∆AMC (g.g).
Suy ra \[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\] (các cạnh tương ứng tỉ lệ).
Vậy AM . AB = AN. AC (đpcm).

