Cho ∆ ABC, M là trung điểm của BC, N là trung điểm của AC. lấy điểm E đối xứng với điểm M qua điểm N. Chứng minh: a) Tứ giác AECM là hình bình hành. b) Tứ giác AEMB là hình bình hình. c) T
49
12/05/2024
Cho ∆ ABC, M là trung điểm của BC, N là trung điểm của AC. lấy điểm E đối xứng với điểm M qua điểm N. Chứng minh:
a) Tứ giác AECM là hình bình hành.
b) Tứ giác AEMB là hình bình hình.
c) Tứ giác AECB là hình thang.
d) Tìm điều kiện của ∆ABC để hình bình hành AECM là hình chữ nhật.
Trả lời
Lời giải
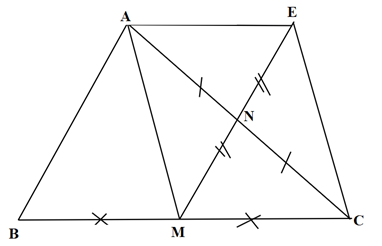
Tứ giác AECM có 2 đường chéo AC và EM cắt nhau tại trung điểm mỗi đường ⇒ Tứ giác AECM là hình bình hành
b) Do tứ giác AECM là hình bình hành ⇒ AE // CM
⇒ AE = CM mà CM = BM (M là trung điểm BC)
⇒ AE = BM
+) AE // CM mà M ∈ BC ⇒ BC // AE và BM // AE
+) Tứ giác AEMB có:
AE = BM
AE // BM
⇒ Tứ giác AEMB là hình bình hành
c) Tứ giác AECB có AE // BC ⇒ Tứ giác AECB là hình thang
d) Để hình bình hành AECM là hình chữ nhật
Thì ^AMC = 90° ⇒ AM là đường cao ΔABC
Mà AM cũng là đường trung tuyến
⇒ ΔABC cân tại A
Vậy để hình bình hành AECM là hình chữ nhật thì ΔABC cân ở A

