Cho ABC đều cạnh a. Gọi I là trung điểm BC. a) Tính vecto AB - vecto AC
Cho DABC đều cạnh a. Gọi I là trung điểm BC.
a) Tính |→AB−→AC|.
b) Tính |→BA−→BI|.
Cho DABC đều cạnh a. Gọi I là trung điểm BC.
a) Tính |→AB−→AC|.
b) Tính |→BA−→BI|.
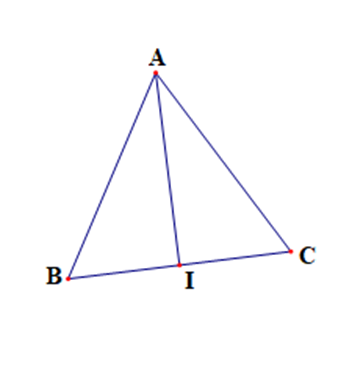
a) Ta có |→AB−→AC|=|→CB|=BC=a
b) Ta có |→BA−→BI|=|→IA|=IA
Vì I là trung điểm của BC nên BI = 12BC = 12a
Vì tam giác ABC đều có AI là trung tuyến
Nên AI là đường cao
Hay AI ⊥ BC
Suy ra tam giác AIB vuông tại I
Do đó AI2 = AB2 – BI2
Hay AI = √a2−(a2)2=a√32
Vậy |→BA−→BI|=a√32.